Tension is the force exerted by a taut rope, but it can be one of the trickiest forces to understand, especially when pulleys are involved. Let's use graphs to break it down and understand tension more clearly!
Dividing the Rope into Sections
Imagine a ball hanging from the ceiling by a rope.
Instead of thinking of the rope as a single unit, we can divide it into smaller sections, as shown in the graph below.
A taut rope exerts the same force (tension) between each of these sections!
For instance, if the tension in the rope is , the purple section in the diagram exerts a downward force of on the red section and an upward force of on the light blue section.

This is the precise understanding of tension. However, when we consider the rope as a whole, most of the tension cancels out. Try turning off the Cancel Forces switch below the graph.

As you can see, when the canceling forces are removed, only the forces at the ends remain. These two forces act on objects other than the rope, so they don't cancel out. The red force at the top pulls on the ceiling, while the green force at the bottom pulls on the ball.
In summary, when analyzing tension, you only need to focus on the two forces exerted at the ends! Of course, these two forces are equal in magnitude.
Special attention is needed when pulleys are involved. Let's explore this next.
Tension on a Pulley
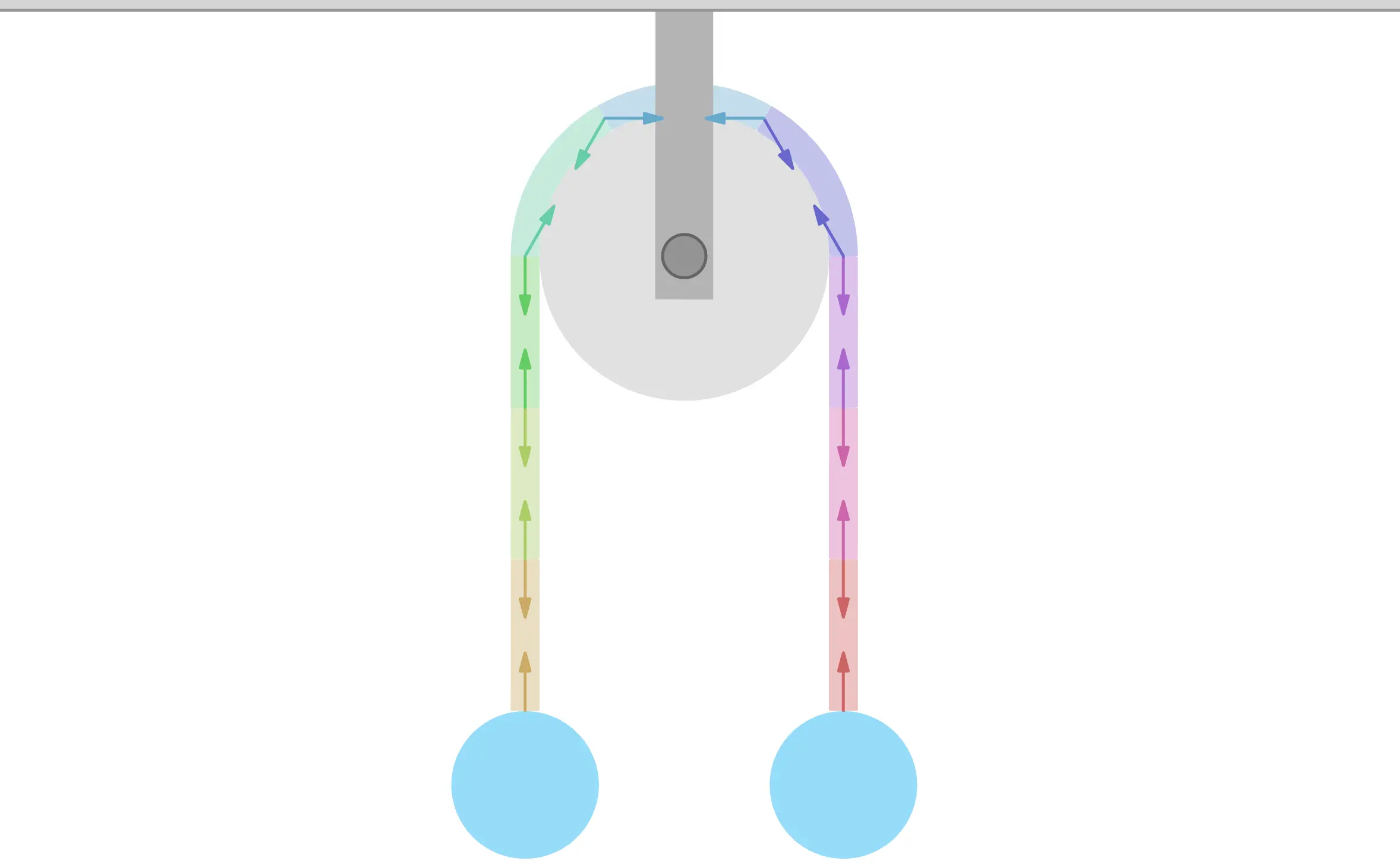
Now, let's consider the force exerted by a rope on a pulley. As shown in the graph below, a rope with balls hanging at both ends is wrapped around a pulley. The rope is divided into sections, just like before.
Again, try removing the canceling forces. Move the Force Display Mode slider to the middle position.

Here's where things get interesting. At the pulley, the rope curves, so the forces don't cancel out! Forces directed toward the pulley remain.
Ultimately, the rope exerts upward forces on the balls at both ends and downward forces on the pulley where it curves.
Technically, the arrows at the curved section represent forces acting on the rope, not the pulley. The rope balances these forces with the normal force exerted by the pulley, keeping it stationary. The pulley, in turn, experiences reaction forces equal to the arrows shown in the diagram.
If the tension in the rope is , it's easy to see that the force on the balls is , but the force on the pulley is less obvious (it requires integration to calculate...). So, think of the rope in contact with the pulley as part of the pulley! Move the graph's slider all the way to the left.

As shown in the diagram above, you can think of the pulley as having two ropes hanging from it!
In this case, the tension acting on the pulley is downward with a magnitude of .


