Are you familiar with Ohm's law?

Ohm's law states that in a resistor, the voltage $V$ and current $I$ are directly proportional, with the resistance $R$ acting as the proportional constant:

This equation describes the relationship between these quantities.

In this section, we'll derive this law using an electrical resistance model. At the same time, we'll observe how electrons behave inside a resistor!

Resistance Model Animation

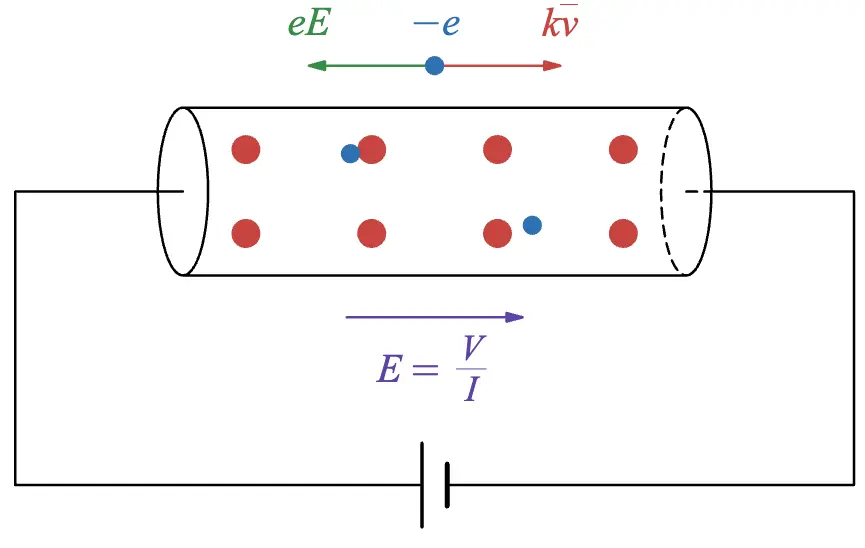
As shown in the animation above, electrons flow through the resistor while colliding with atomic nuclei.

Here's a simplified explanation: the battery creates an electric field directed to the right inside the resistor. Electrons, being negatively charged, experience a force in the opposite direction of the electric field. They accelerate to the left but are slowed down by collisions with atomic nuclei. Eventually, the electric field's force and the resistance force balance out, causing the electrons to flow to the left at a steady average velocity.

Now, let's dive deeper into the details!

Deriving Ohm's Law

Electric Field Generation

When a battery with an electromotive force $V\,[\mathrm{V}]$ is connected, a uniform electric field $E\,[\mathrm{N/C}]$ is created inside the resistor.

If the resistor's length is $l\,[\mathrm{m}]$, the electric field's magnitude is given by:

The electric field's magnitude equals the potential gradient's magnitude.

Force Due to the Electric Field

The electric field exerts a force on electrons. If an electron's charge is $-e\,[\mathrm{C}]$, the force's magnitude is:

The force's direction is opposite to the electric field.

Under this force, electrons move to the left.

Resistance Force from Atomic Nuclei

If only the electric field's force acted, electrons would keep accelerating. However, in reality, they slow down due to frequent collisions with atomic nuclei inside the resistor (as shown in the animation).

Precisely describing this behavior is challenging. However, we can assume that the faster the electrons move, the more collisions they experience. On average, this results in a resistance force proportional to their speed.

If the proportional constant is $k\,[\mathrm{N\cdot s/m}]$, the resistance force can be expressed as:

Here, $\bar v\,[\mathrm{m/s}]$ represents the electrons' average speed.

Force Balance

In the steady state, the electric field's force and the resistance force balance out, resulting in a constant velocity.

Thus, the force balance equation is:

From this, the electrons' average speed is:

Current and Electron Speed Relationship

When electrons move to the left with an average speed of $\bar v\,[\mathrm{m/s}]$, a current of magnitude:

flows to the right. Here, $n\,[\mathrm{/m^3}]$ is the electron number density, and $S\,[\mathrm{m^2}]$ is the resistor's cross-sectional area.

Ohm's Law

Thus, the current's magnitude is:

Rearranging this gives:

This shows that $I$ and $V$ are proportional!

Here, $\rho=\dfrac k{ne^2}$ is called the resistivity, and $R=\rho\dfrac{l}{S}$ is the resistance. Using these, we find:

This is Ohm's law.

Real-World Behavior

This resistance model is based on Newtonian mechanics. However, in reality, electrons follow quantum mechanics, which is more complex and beyond the scope of this explanation.