Have you ever wondered at what angle you should launch an object to make it travel the farthest? Let's find out with a simulation!
We'll also explore what happens when air resistance is taken into account.
Simulating Parabolic Motion START / STOP
Adjust the launch angle and see how far the object travels. Can you find the angle that gives the maximum distance?
By pressing the START/STOP button and experimenting with different angles, you'll discover that the object travels the farthest at 45 ∘ 45^\circ 4 5 ∘
Let's Do the Math Now, let's calculate the distance the object travels!
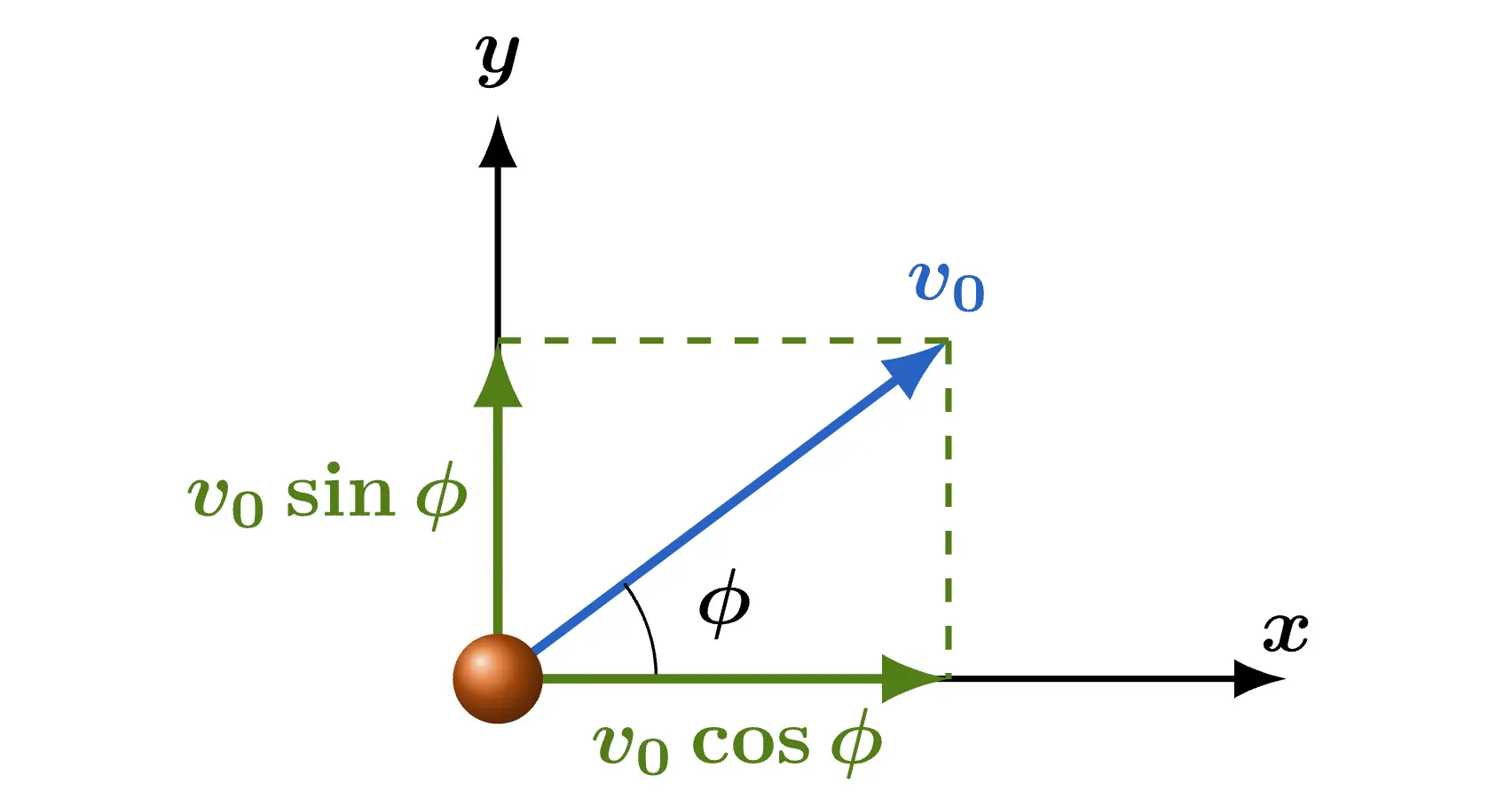
Imagine throwing a ball with a launch angle ϕ \phi ϕ v 0 v_0 v 0 g g g
In the y y y v 0 sin ϕ v_0\sin \phi v 0 sin ϕ t t t
a y ( t ) = − g ∴ v y ( t ) = v 0 sin ϕ + ∫ 0 t a y ( t ) d t = v 0 sin ϕ − g t ∴ y ( t ) = ∫ 0 t v y ( t ) d t = ( v 0 sin ϕ ) t − 1 2 g t 2
\begin{align*}
a_y(t)&=-g\\
\therefore\ v_y(t)&=v_0\sin\phi +\int_0^ta_y(t)dt=v_0\sin\phi-gt\\
\therefore\ y(t)&=\int_0^tv_y(t)dt=(v_0\sin\phi )t-\frac12gt^2
\end{align*}
a y ( t ) ∴ v y ( t ) ∴ y ( t ) = − g = v 0 sin ϕ + ∫ 0 t a y ( t ) d t = v 0 sin ϕ − g t = ∫ 0 t v y ( t ) d t = ( v 0 sin ϕ ) t − 2 1 g t 2 The time t 1 t_1 t 1
y ( t 1 ) = 0 ∴ t 1 = 2 v 0 sin ϕ g ( ≠ 0 ) y(t_1)=0\quad\therefore\ t_1=\frac{2v_0\sin\phi}g\ (\neq 0) y ( t 1 ) = 0 ∴ t 1 = g 2 v 0 sin ϕ ( = 0 ) as derived above!
In the x x x v 0 cos ϕ v_0\cos\phi v 0 cos ϕ L L L t 1 t_1 t 1
L = ( v 0 cos ϕ ) t 1 = 2 v 0 2 sin ϕ cos ϕ g = v 0 2 sin 2 ϕ g L=(v_0\cos\phi)t_1=\frac{2v_0^2\sin\phi\cos\phi}g=\frac{v_0^2\sin2\phi}g L = ( v 0 cos ϕ ) t 1 = g 2 v 0 2 sin ϕ cos ϕ = g v 0 2 sin 2 ϕ as derived above.
Therefore, the angle ϕ \phi ϕ L L L ϕ = π 4 \phi=\dfrac{\pi}{4} ϕ = 4 π
Adding Air Resistance (Advanced) What happens to parabolic motion when air resistance is included?
Modeling air resistance accurately is challenging, but it can generally be divided into two types: viscous resistance , which is proportional to velocity, and inertial resistance , which is proportional to the square of velocity.
Here, we'll consider a case where only viscous resistance acts. Let the proportional constant be k k k k ∣ v → ∣ k|\overrightarrow v| k ∣ v ∣
m d v x d t = − k v x m d v y d t = − k v y − m g
\begin{align*}
m\frac{dv_x}{dt}&=-kv_x\\[8px]
m\frac{dv_y}{dt}&=-kv_y-mg\\
\end{align*}
m d t d v x m d t d v y = − k v x = − k v y − m g as shown above.
Solving the first equation gives:
d v x d t = − k m v x ∴ v x = C 0 e − ( k / m ) t \frac{dv_x}{dt}=-\frac km v_x\quad\therefore\ v_x=C_0e^{-(k/m)t} d t d v x = − m k v x ∴ v x = C 0 e − ( k / m ) t Since v x ( 0 ) = v 0 cos ϕ v_x(0)=v_0\cos\phi v x ( 0 ) = v 0 cos ϕ C 0 = v 0 cos ϕ C_0=v_0\cos\phi C 0 = v 0 cos ϕ
v x = ( v 0 cos ϕ ) e − ( k / m ) t x = ∫ 0 t v x d t = m v 0 cos ϕ k ( 1 − e − ( k / m ) t ) \begin{align*}
v_x&=(v_0\cos\phi)e^{-(k/m)t}\\[5px]
x&=\int_0^tv_xdt=\frac{mv_0\cos\phi}{k}(1-e^{-(k/m)t})
\end{align*} v x x = ( v 0 cos ϕ ) e − ( k / m ) t = ∫ 0 t v x d t = k m v 0 cos ϕ ( 1 − e − ( k / m ) t ) Thus, the x x x
Solving the second equation gives:
d v y d t = − k m ( v y + m g k ) ∴ v y + m g k = C 1 e − ( k / m ) t \begin{align*}
\frac{dv_y}{dt}=-\frac km \left(v_y+\frac{mg}{k}\right)\\[10pt]
\quad\therefore\ v_y+\frac{mg}{k}=C_1e^{-(k/m)t}
\end{align*} d t d v y = − m k ( v y + k m g ) ∴ v y + k m g = C 1 e − ( k / m ) t Since v y ( 0 ) = v 0 sin ϕ v_y(0)=v_0\sin\phi v y ( 0 ) = v 0 sin ϕ C 1 = v 0 sin ϕ C_1=v_0\sin\phi C 1 = v 0 sin ϕ
v y = ( v 0 sin ϕ ) e − ( k / m ) t − m g k y = ∫ 0 t v y d t = m v 0 sin ϕ k ( 1 − e − ( k / m ) t ) − m g k t \begin{align*}
v_y&=(v_0\sin\phi)e^{-(k/m)t}-\frac{mg}{k}\\[5px]
y&=\int_0^tv_ydt=\frac{mv_0\sin\phi}{k}(1-e^{-(k/m)t})-\frac{mg}{k}t
\end{align*} v y y = ( v 0 sin ϕ ) e − ( k / m ) t − k m g = ∫ 0 t v y d t = k m v 0 sin ϕ ( 1 − e − ( k / m ) t ) − k m g t Thus, the y y y
Simulating Parabolic Motion (With Air Resistance) Here's a simulation for this scenario!
START / STOP
Depending on the strength of the resistance force, the optimal launch angle for maximum distance might be less than 45 ∘ 45^\circ 4 5 ∘