Have you ever heard of the Monkey Hunting problem?

It's a famous and fascinating problem that can be understood with basic mechanics.

Let's explore Monkey Hunting using a graph!

What is Monkey Hunting?

Monkey Hunting involves a scenario where a monkey hanging from a tree is targeted with a gun.

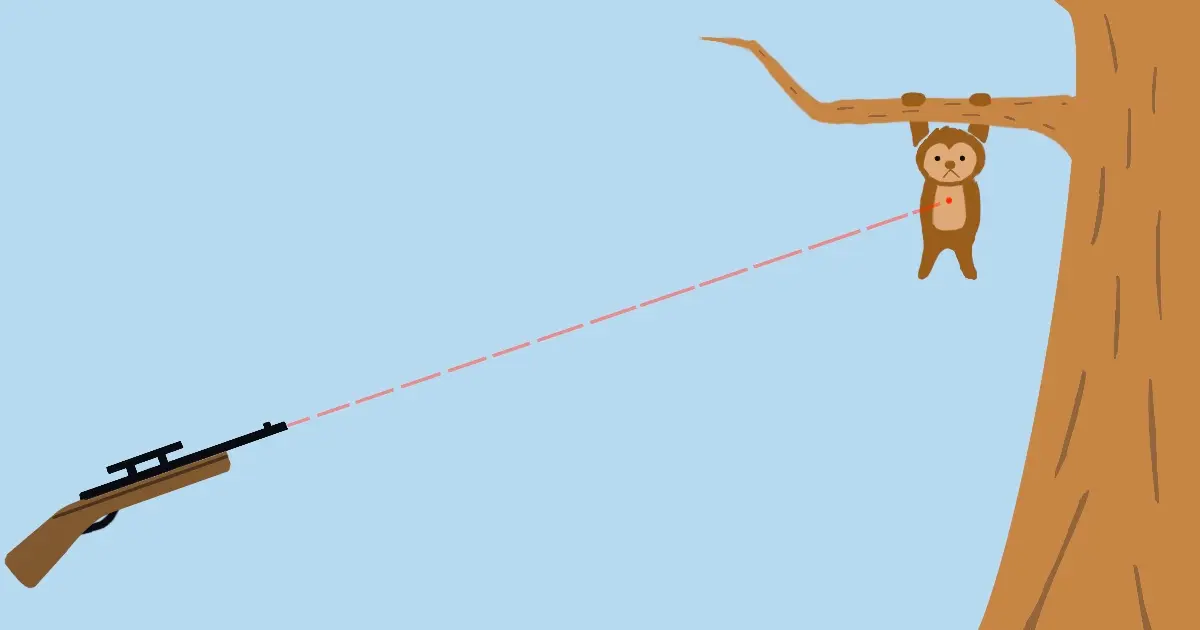
(Don't worry, this is just a thought experiment...)

Here's the twist: the monkey is assumed to let go and start falling the moment it hears the gunshot.
(For simplicity, we ignore the speed of sound and assume an ideal situation where the monkey lets go at the exact moment the gun is fired.)

The question is: where should you aim to hit the monkey? This is the Monkey Hunting problem.

Intuitively, you might think you need to aim slightly above the monkey to account for the bullet's drop due to gravity.

Let's test this idea and see what happens!

Let's Try It

(In reality, the bullet might hit the ground, but we'll ignore that for now.)

After experimenting a few times, you might notice the conditions needed to hit the monkey.

The result is surprising: to hit the monkey, you should aim directly at it. The firing speed doesn't matter at all. As long as you aim at the monkey, you'll always hit it.

This result might seem counterintuitive.
Let's explore why this happens.

Why You Should Aim Directly

We'll explain this with two approaches: one using equations and another using a free-fall frame of reference.

Proof Using Equations

Let the accelerations of the bullet and the monkey be $a_{\textrm{bullet}},\ a_{\textrm{monkey}}$, and let the gravitational acceleration be $g$.

Since both the bullet and the monkey are only affected by gravity,

and they both experience uniformly accelerated motion in the $y$ direction.

Therefore, the $y$ coordinates of the bullet and the monkey at time $t$ are given by the equations of uniformly accelerated motion:

(You can also derive this by integrating acceleration twice with respect to time.)

In the $x$ direction, the bullet moves with a constant velocity of $v_0\cos{\theta}$, so the time $t_1$ when the $x$ coordinates of the bullet and the monkey are equal is:

(Here, $r$ is the initial horizontal distance between the monkey and the bullet.)

At this time, if their $y$ coordinates are also equal, they will collide. This condition is:

This proves that you should aim directly at the monkey to hit it!

Proof Using a Free-Fall Frame

Without doing the calculations above, the reason becomes clear when viewed from the perspective of an observer who is free-falling along with the bullet and the monkey.

To this observer, the bullet and the monkey appear unaffected by gravity (similar to how objects inside a falling elevator appear weightless!).
The monkey appears stationary, and the bullet moves in a straight line at a constant speed in the direction it was fired.

Thus, the bullet will hit the monkey only if the gun is aimed directly at it.