Thomson's experiment and the magnetic deflection experiment allow us to determine the Specific Charge, which is the ratio of an electron's charge to its mass. Let's explore these experiments through animations!

Animation

Overview of the Experiments

Both experiments aim to achieve the same goal in slightly different ways.

First, electrons are emitted from the left. In Thomson's experiment, an electric field is used, while in the magnetic deflection experiment, a magnetic field is applied to bend the electrons' trajectory. Finally, the position where the electrons hit the screen is measured.

From these measurements, the charge-to-mass ratio of the electron can be calculated. Let's take a closer look at each experiment!

Thomson's Experiment

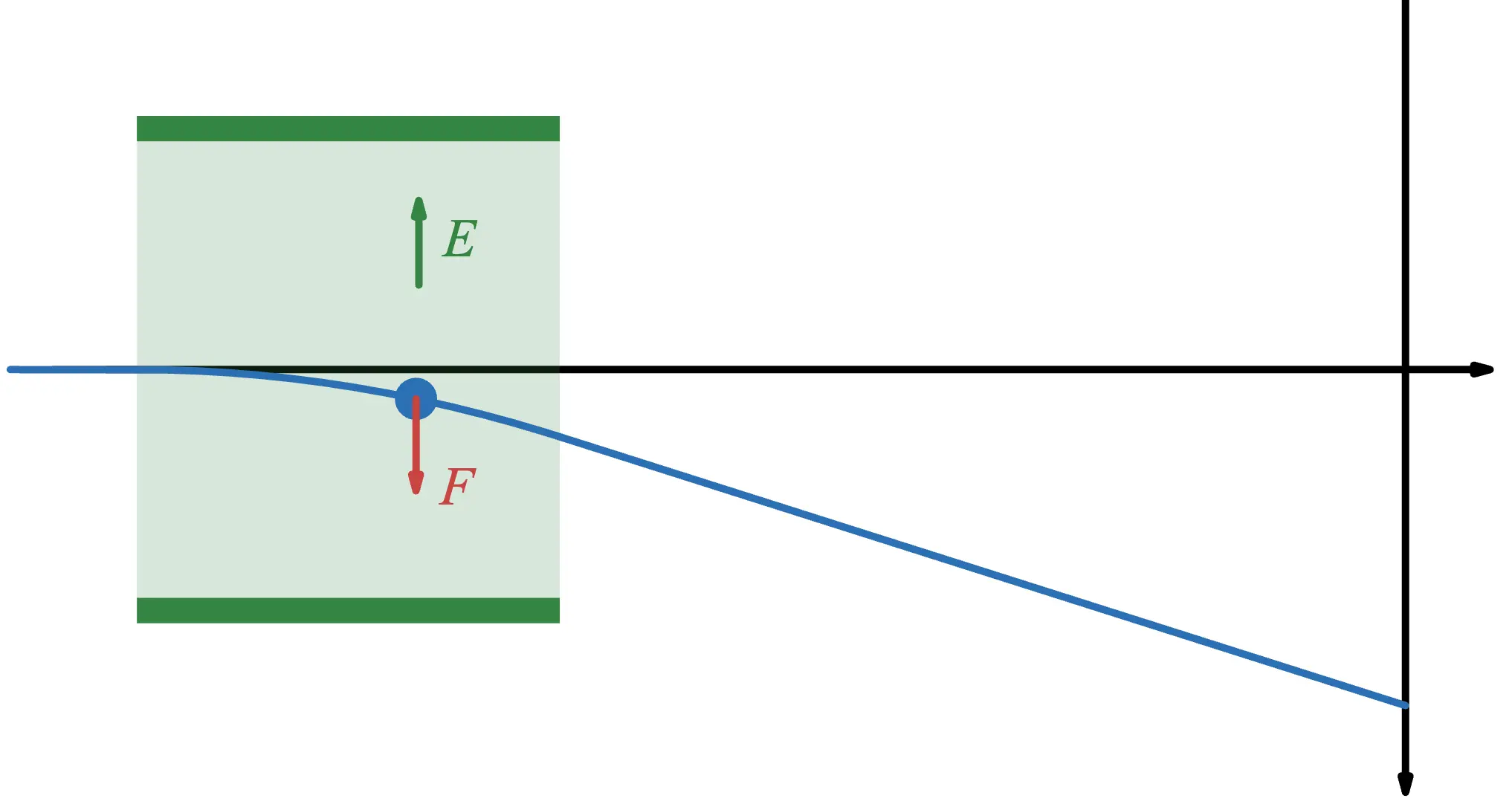
In Thomson's experiment, an electric field is used to apply force to the electrons. By placing metal plates with different potentials, a uniform electric field is created between them, and electrons are passed through this field.

The dark green areas represent the metal plates, while the light green areas indicate the regions where the electric field is present. You can think of it as a capacitor.

Electrons experience a force due to the electric field. Since electrons are negatively charged, the force acts in the direction opposite to the electric field.

The gravitational force acting on the electron is negligible compared to the electric force and can be ignored.

Since the force always acts downward, if we take the downward direction as positive, the equation of motion becomes:

Here, $m$ is the mass of the electron, $-e$ is the charge of the electron, $a$ is the downward acceleration, and $E$ is the magnitude of the electric field.

From this, we get:

This means the electron undergoes uniform acceleration. This is similar to an object experiencing gravity, so the electron follows a parabolic trajectory.

Once the electron exits the electric field region, it no longer experiences any force. It moves in a straight line at a constant velocity until it reaches the screen.

If the length of the electric field region is $l$ and the initial velocity is $v_0$, the vertical distance the electron travels within the electric field region is:

In the region beyond the electric field, the vertical distance traveled depends on the vertical velocity of the electron, which is $\dfrac{eE}{m}\dfrac l{v_0}$, and is given by:

Here, $L$ is the length of this region.

Therefore, the total vertical position $y_0$ where the electron hits the screen is the sum of these distances:

Rearranging this gives:

This equation allows us to calculate the charge-to-mass ratio $e/m$ from the measurements!

Magnetic Deflection Experiment

In the magnetic deflection experiment, a magnetic field is used to bend the electrons' trajectory. A region with a magnetic field is created, and electrons are directed into it.

Electrons experience a Lorentz force due to the magnetic field. Unlike the electric force, the Lorentz force acts perpendicular to the direction of motion, causing the electrons to move in a circular path while maintaining a constant speed.

From the equation of motion in the radial direction:

Here, $r$ is the radius of the circular motion. Now, define the angle $\theta$ as shown below:

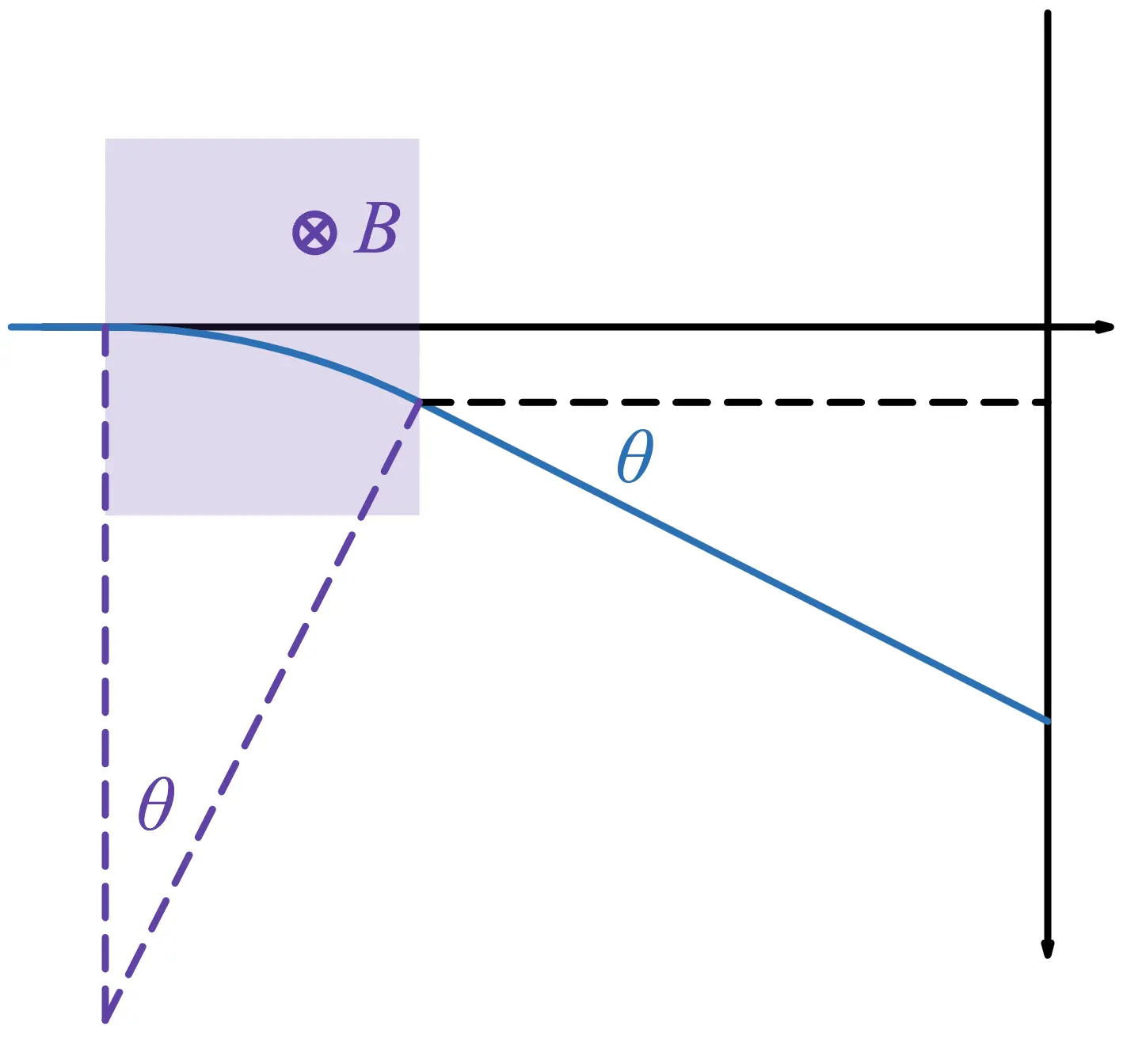
From the diagram:

If $y_0$ is the position where the electron hits the screen, then:

Assuming $r\gg l$ and $\theta\ll 1$, we can approximate:

Using this approximation:

Rearranging this gives:

This equation allows us to calculate the charge-to-mass ratio $e/m$ from the measurements!

Significance of the Charge-to-Mass Ratio

The mass and charge of an electron are extremely small and difficult to measure directly. However, these experiments provide a way to determine the charge-to-mass ratio $e/m$.

In the 20th century, Millikan's oil drop experiment successfully determined the elementary charge $e$. Using this value and the charge-to-mass ratio, the mass of the electron $m$ was also calculated.