One of the key characteristics of waves is their ability to reflect when they hit a wall. Let's explore the fascinating phenomenon of wave reflection!
What is Reflection?
The basics of reflection involve three main concepts: "incident wave," "reflected wave," and "composite wave".
The wave that strikes the wall is called the incident wave, while the wave that bounces back is known as the reflected wave. What we actually observe is the superposition of the incident wave and the reflected wave (principle of superposition), and this combined wave is referred to as the composite wave.
The type of reflected wave determines the nature of the composite wave we see. Broadly, there are two types of reflection: "free-end reflection" and "fixed-end reflection".
Before diving into the details, let's interact with the graph below to observe the differences!
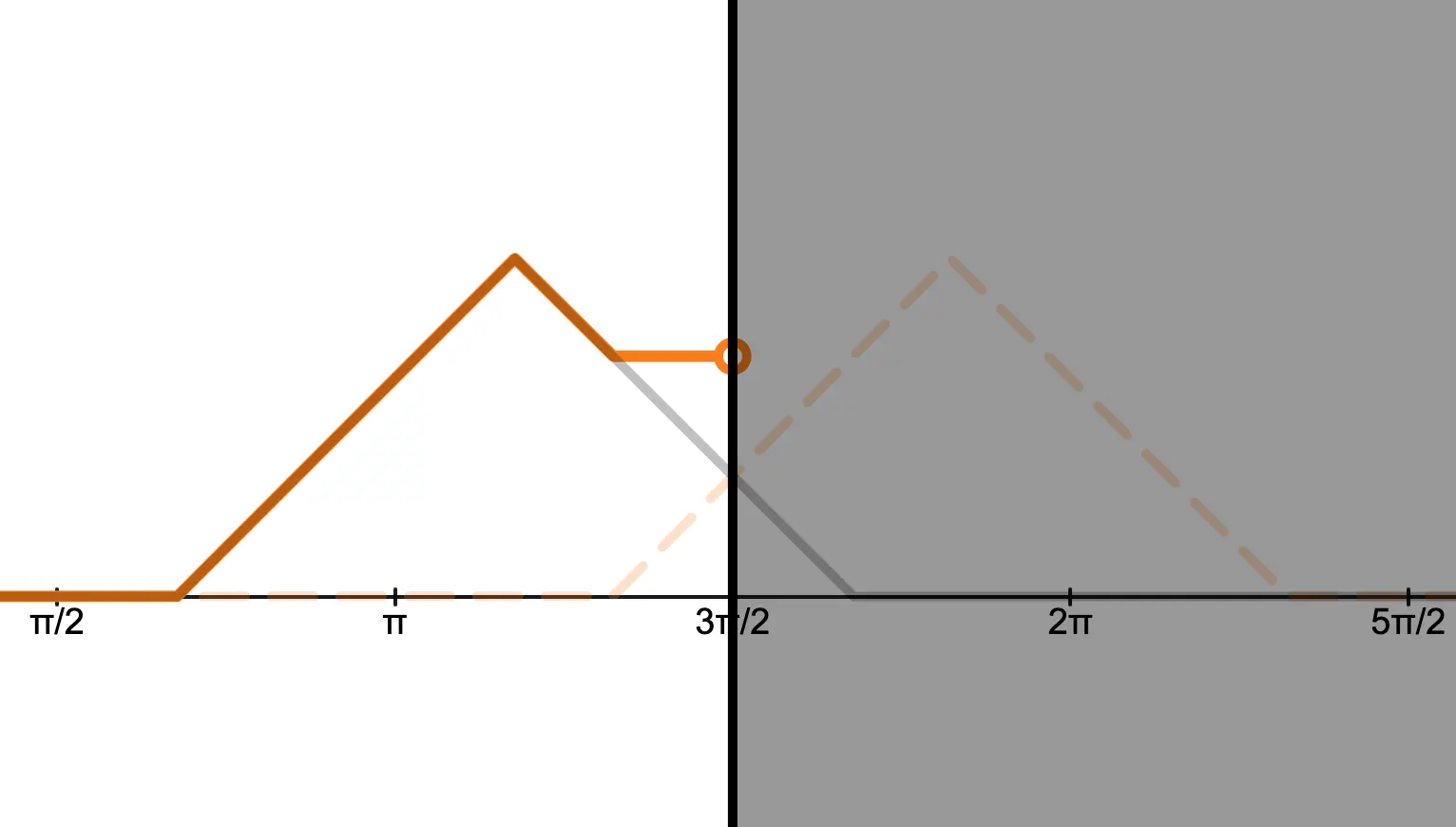
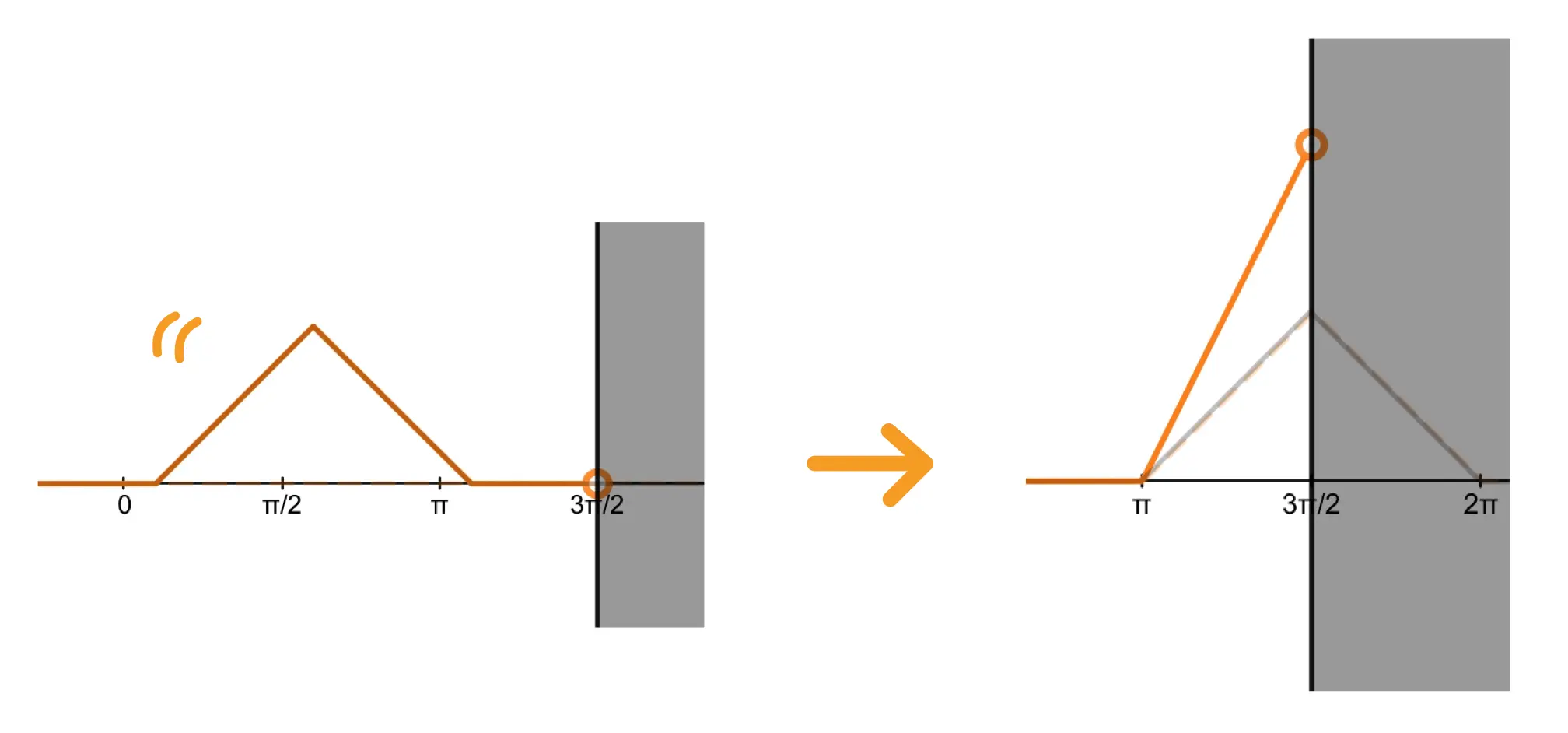
Graph of Triangle Wave Reflection
The graph below illustrates the free-end and fixed-end reflections of a triangular wave (commonly called a triangle wave).
Try to spot the differences between free-end and fixed-end reflections!
Incident Wave | Reflected Wave | Composite Wave |
|---|---|---|
(Dotted) | (Solid) |
Differences Between Free-End and Fixed-End Reflection
The primary difference between free-end and fixed-end reflection lies in whether the displacement of the composite wave at the reflector (the white circle on the graph) is free to move or fixed in place. As the names suggest, the end of the wave is either free or fixed.
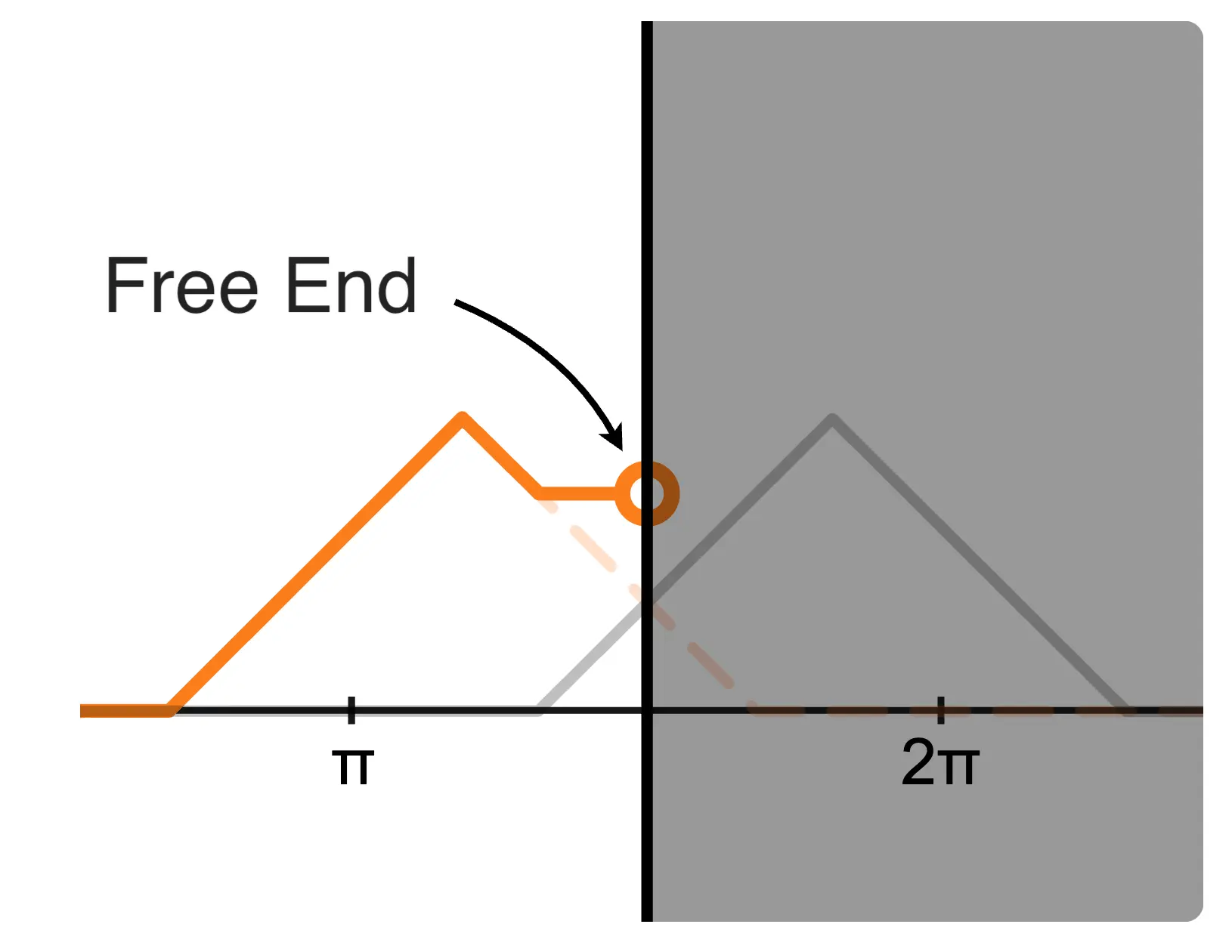
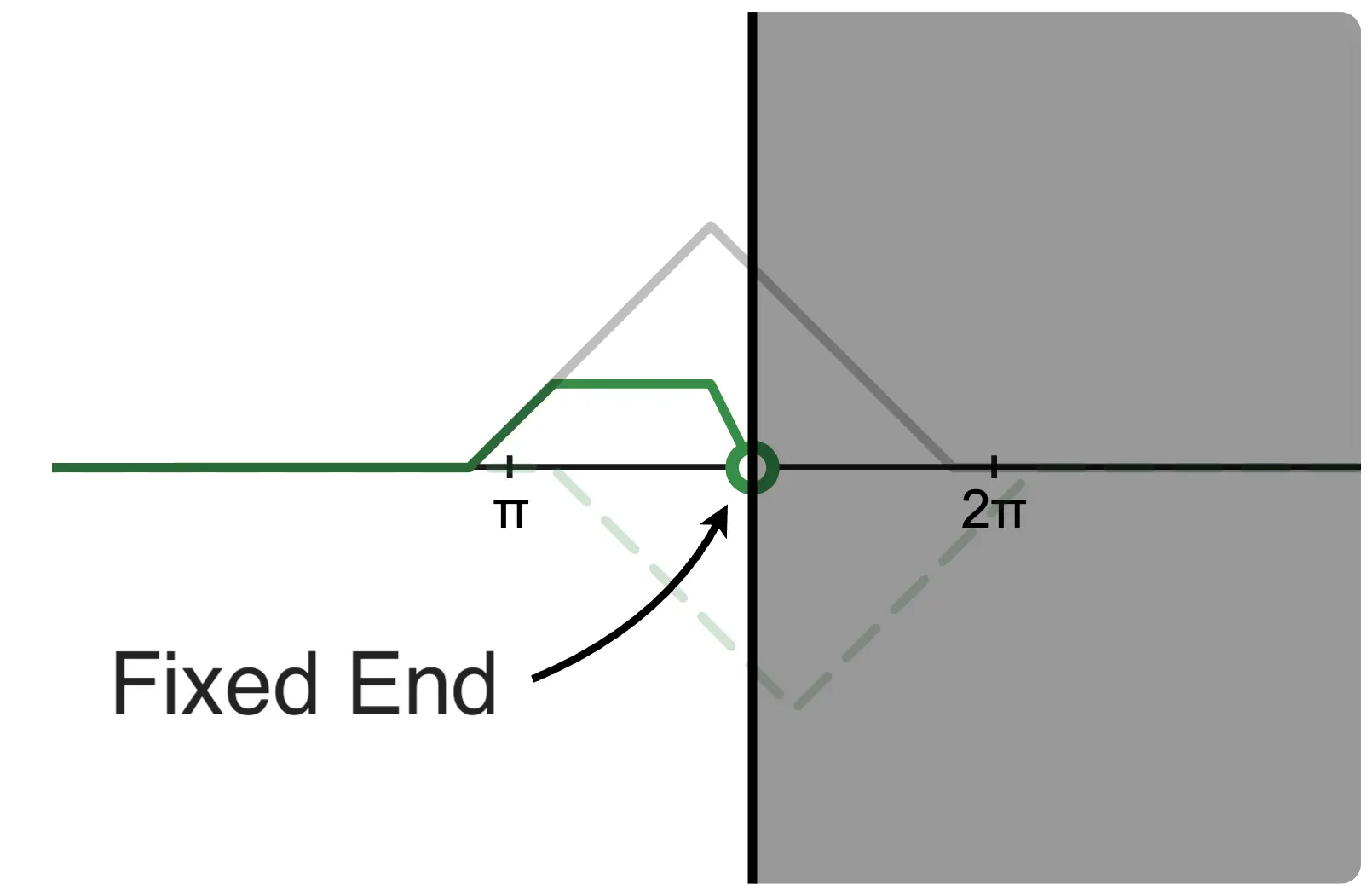
The cause of this difference lies in the reflected wave.
In free-end reflection, the reflected wave is symmetric to the incident wave with respect to the reflector. In fixed-end reflection, the reflected wave is point-symmetric to the incident wave with respect to the center of the reflector. (In fixed-end reflection, the phase of the reflected wave can be considered to shift by .)
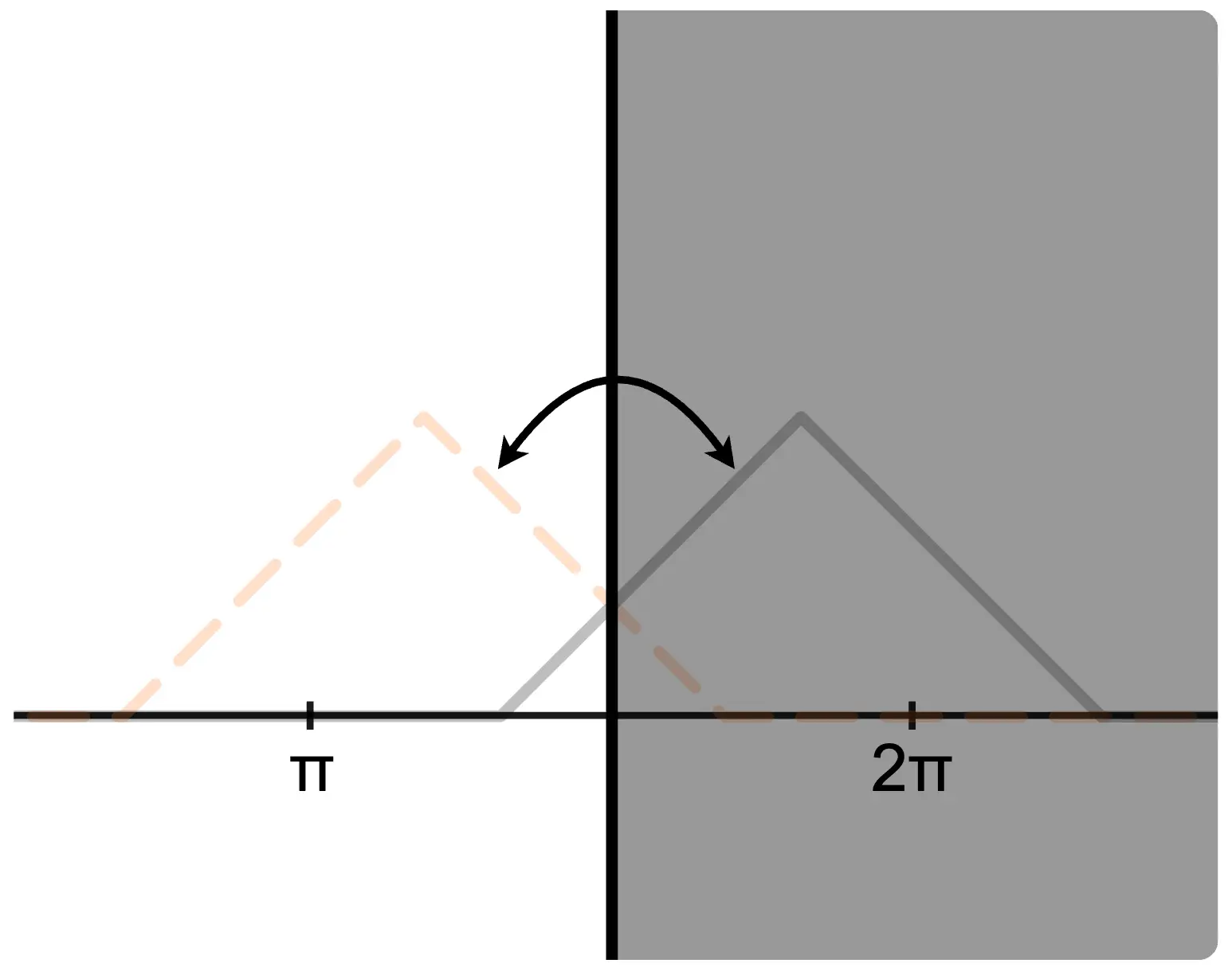
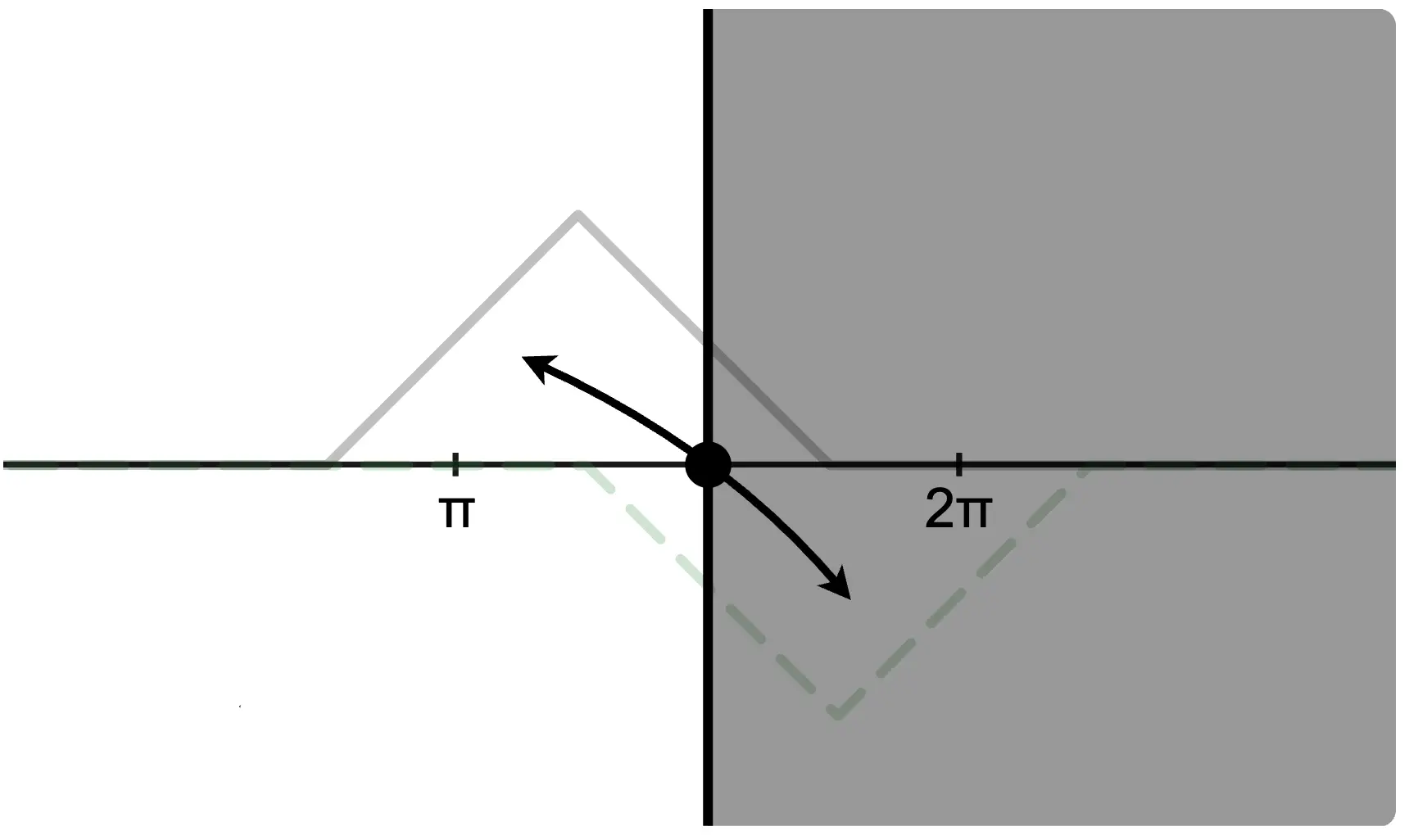
Thus, the type of reflection—free-end or fixed-end—is determined by the nature of the reflected wave.
Next, let's examine the reflection of sine waves!
Graph of Sine Wave Reflection
You can drag the wave source left and right to observe its behavior!
Source | Incident Wave | Reflected Wave | Composite Wave |
|---|---|---|---|
● | (Dotted) | (Solid) |
Similarly, sine waves also exhibit free-end and fixed-end reflections.
In both cases, standing waves are formed, which is an important concept to note!
We'll delve deeper into their properties in the next session!
Examples of Free-End and Fixed-End Reflection
Here are some real-world examples of these types of reflections. For instance, consider a rope with one end held by hand and the other tied to a pole.
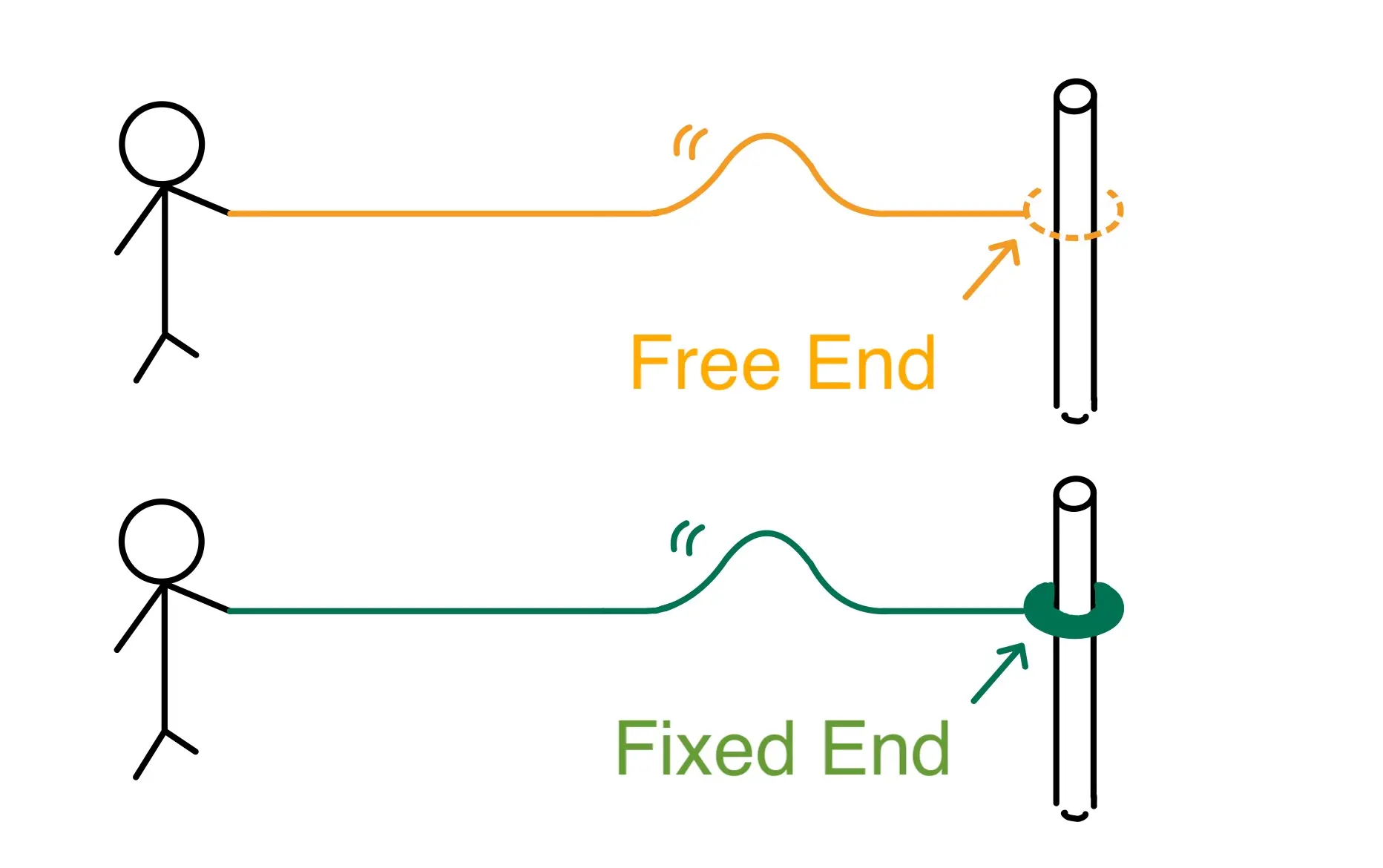
In this scenario, as shown in the figure above, the way the rope reflects depends on whether the end tied to the pole can move freely along the pole.
Another example is water surface waves, which undergo free-end reflection. When waves hit the wall of a pool, large waves are formed, as shown in the figure. (You can observe this behavior in the graph above.)
For light waves, the type of reflection depends on the refractive index and can be either free-end or fixed-end. We'll explore this in another article.
For sound waves, which are longitudinal waves, the situation is more complex. This complexity has even led to errors in university entrance exam questions, such as those at Osaka University. We'll cover this topic in detail in a future article.


