Here are some key points about free-end and fixed-end reflection of sine waves that are often asked in exams.

If you're wondering what free-end and fixed-end reflection are, read this article first!

Exploring Fixed-End and Free-End Reflection with Graphs

Graph of Sine Wave Reflection

Here is the graph of sine wave reflection that was also included in the previous article!

The key points to remember are as follows:

Let's explain each of these points.

The Section Between the Wave Source and the Reflector (Important)

Characteristics

In the section between the wave source and the reflector, the incident wave and the reflected wave with the same wavelength and amplitude travel in opposite directions, resulting in a standing wave.

As mentioned in the supplement, when the incident wave has a wavelength of $\lambda$ and an amplitude of $A$, the resulting standing wave will have a wavelength of $\lambda$ and an amplitude of $2A$.

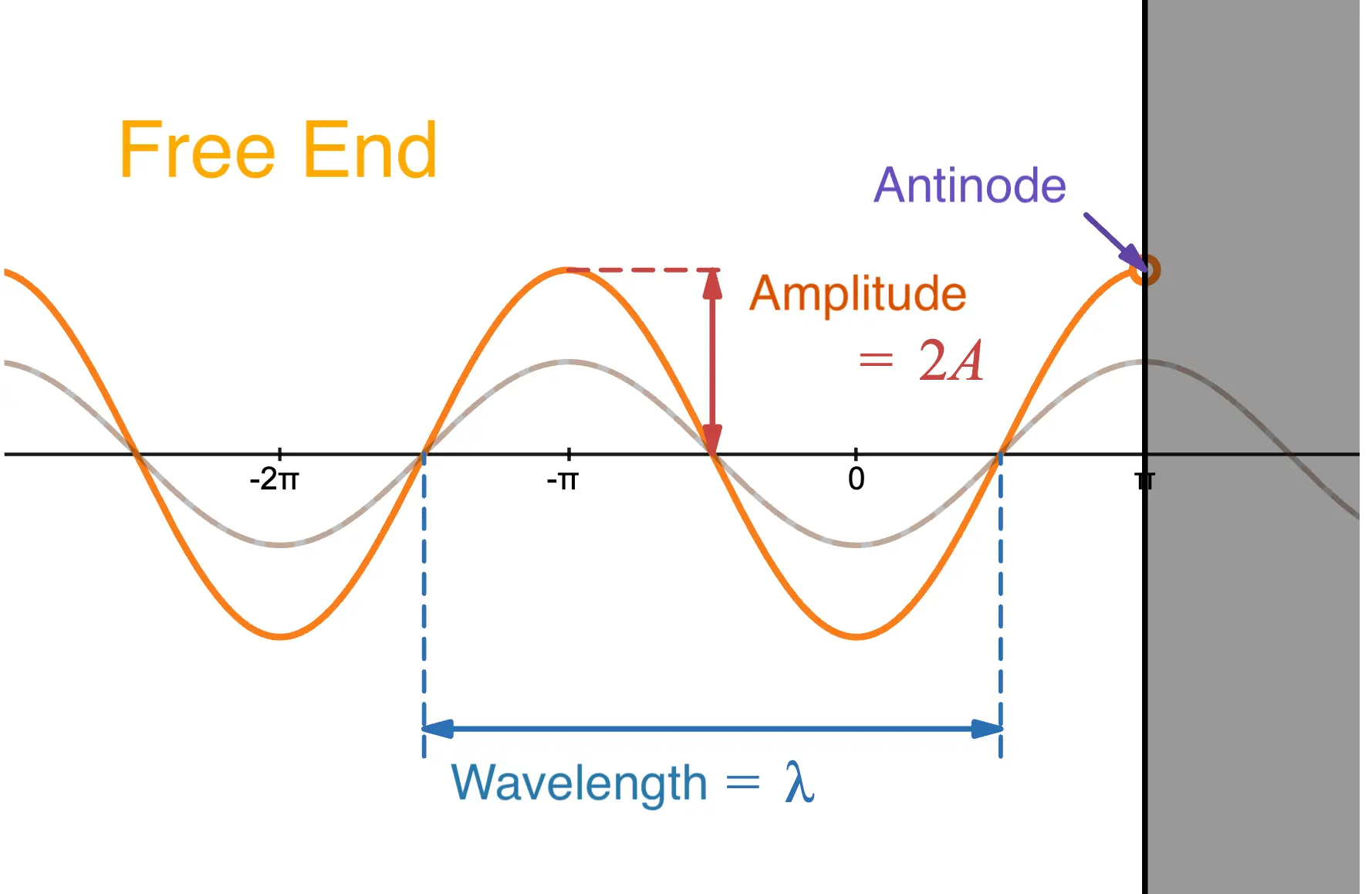
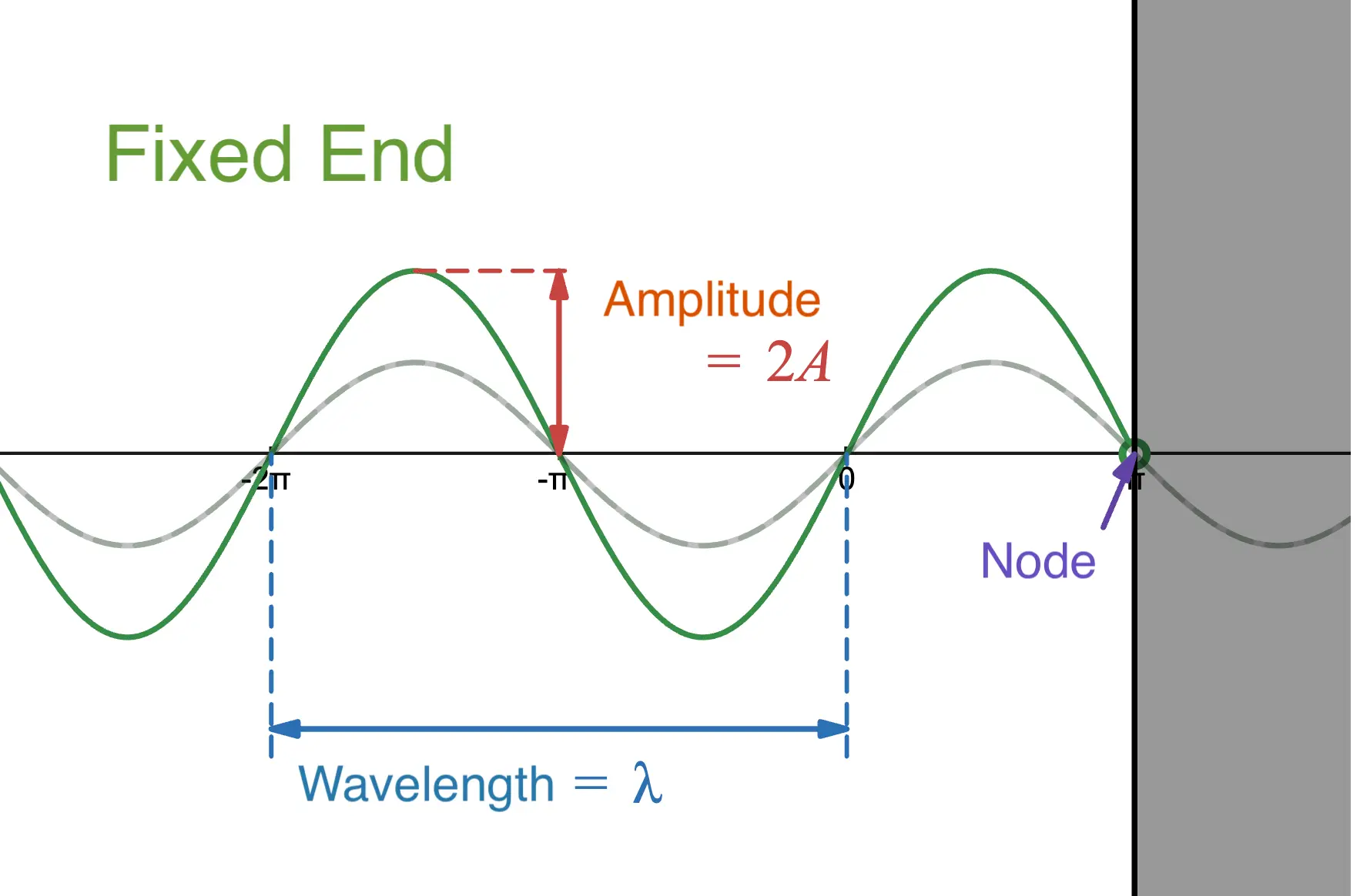
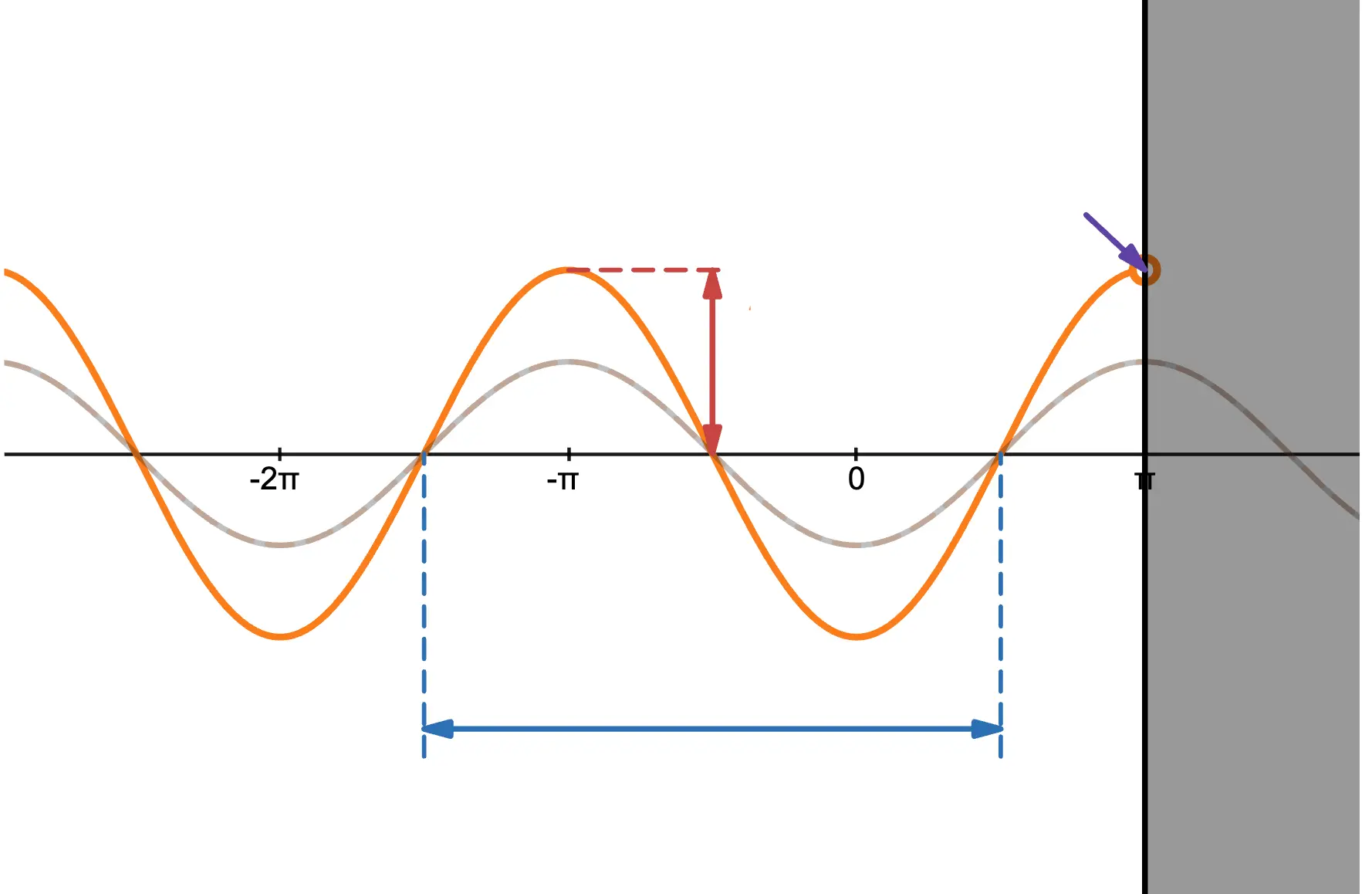
The key point is that the medium at the reflector becomes an antinode in the case of free-end reflection and a node in the case of fixed-end reflection (see the images above for reference!).

As mentioned in the supplement, an antinode is the point of maximum amplitude in a standing wave (in this case, a point with an amplitude of $2A$). This is why the end moves freely, resulting in free-end reflection.

Similarly, a node is a point in a standing wave that does not oscillate at all, so the end does not move at all, resulting in fixed-end reflection.

Equation of the Composite Wave

It is also important to be able to calculate the equation of the composite wave.

Consider the case where the incident wave is expressed as:

Here, $A,\,\lambda ,\,T$ represent the amplitude, wavelength, and period, respectively.

In the Case of Free-End Reflection

First, let's determine the equation of the reflected wave.

As shown in the figure above, the reflected wave is symmetric to the incident wave with respect to the wall.

Therefore, the displacement $y_{\textrm{reflected}}(x,\,t)$ of the reflected wave at position $x$ is equal to the displacement $y_{\textrm{incident}}(2l-x,\,t)$ of the incident wave at position $2l-x$ (where $x,\ 2l-x$ are symmetric about the wall at $l$).

Thus, the reflected wave can be expressed as:

The composite wave is the sum of the incident wave and the reflected wave, so:

This is the equation of the composite wave! (The sum-to-product formula was used in the final step.)

In the Case of Fixed-End Reflection

First, let's determine the reflected wave. Unlike free-end reflection, the reflected wave is also symmetric in the vertical direction (in addition to the horizontal direction), resulting in point symmetry.

Thus, the reflected wave is the negative of the reflected wave in the case of free-end reflection:

(A negative sign is added.)

The composite wave is the sum of the incident wave and the reflected wave, so:

This is the equation of the composite wave!

The Section Beyond the Wave Source

Beyond the wave source, the incident wave and the reflected wave with the same wavelength and amplitude travel in the same direction, resulting in a traveling wave (i.e., a regular sine wave).

The wavelength is the same as that of the traveling wave, which is straightforward. However, the amplitude requires attention.

Unlike standing waves, traveling waves have the same amplitude at all points. Therefore, the amplitude at the position of the wave source is equal to the amplitude of the traveling wave.

As shown in the graph above, the traveling wave and the standing wave are continuous (i.e., connected) at the position of the wave source! Thus, the amplitude of the standing wave at the position of the wave source matches the amplitude of the traveling wave.

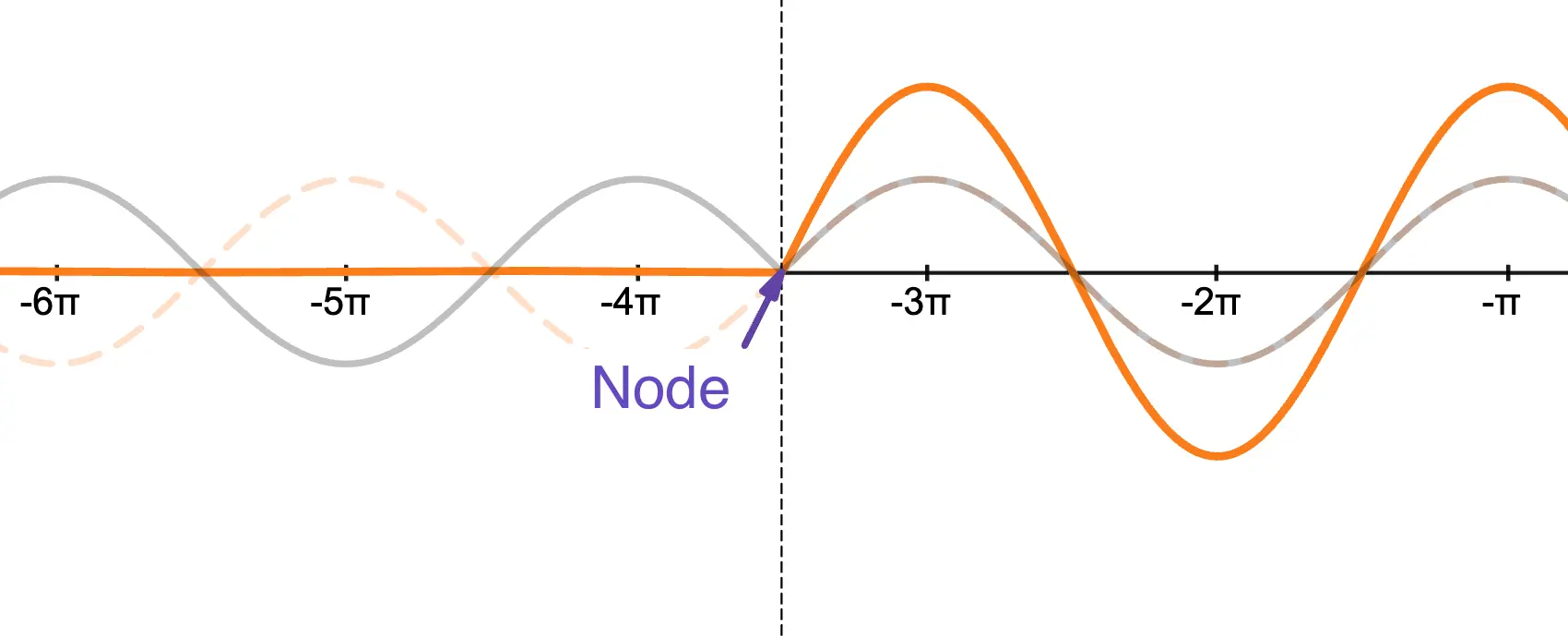
In other words, the amplitude depends on the distance between the wave source and the reflector. As shown in the figure below, if the wave source is at a node of the standing wave, no wave is generated.