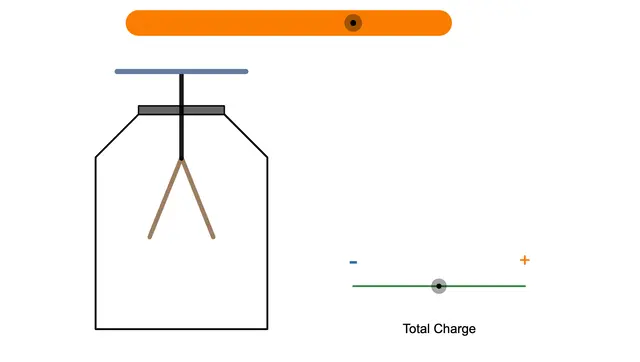
Have you ever heard of the kinetic theory of gases? Let's explore how gas molecules behave using simulations and graphs! Afterward, we'll dive into the relationship between gas molecules and pressure.

Animation

This animation shows the motion of countless gas molecules bouncing around inside a container. Use the Add and Remove buttons to add or remove gas molecules.

Keep in mind that intermolecular forces are ignored here. The gas molecules only collide elastically with the walls of the container.

By the way, you can switch the graph's colors to black and white from the settings in the top-right corner. It looks pretty cool—give it a try!

Behavior of Gas Molecules

In the air around us, countless tiny gas molecules are moving invisibly.

On Earth, gravity pulls objects downward. However, for extremely light particles like gas molecules, gravity's effect is negligible. This allows them to move freely in all directions, seemingly defying gravity.

Gas Pressure

What is Gas Pressure?

So, what exactly is gas pressure?

As the name suggests, gas pressure is the "pressure exerted by a gas." Pressure is defined as force divided by area. In simpler terms, gas pressure measures how much force gas molecules exert on the walls of a container per unit area. Let's use the animation to understand this better.

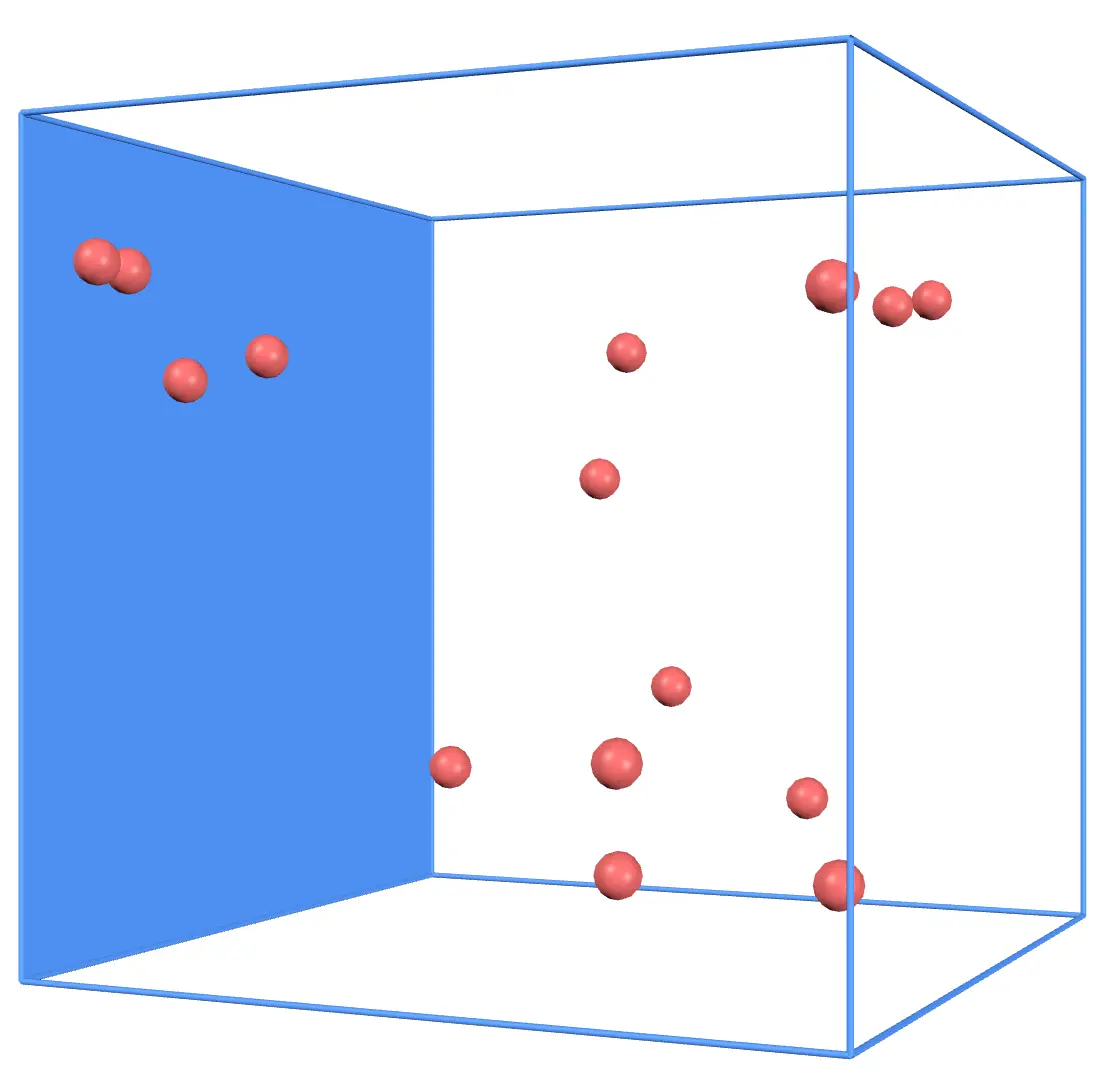
Take a look at one wall of the container, as shown in the image above.

Gas molecules collide with this wall, exerting force on it. On average, each gas molecule exerts a force of

(Derivation omitted). Here, $m$ is the mass of one gas molecule, $\overline{v^2}$ is the average of the square of the speed of gas molecules, and $l$ is the length of one side of the container.

If there are $N\ [\textrm{molecules}]$ of gas molecules, the total force exerted by all molecules is

The gas pressure is this force divided by the wall area $l^2$ . Thus,

is the gas pressure. Here, the container's volume is $V\,(=l^3)$. The unit of pressure is $\mathrm{Pa}$Pascal$=\mathrm{N/m^2}$ .

Properties of Gas Pressure

Let's explore the properties of gas pressure using the animation and the formula:

Here are some key points:

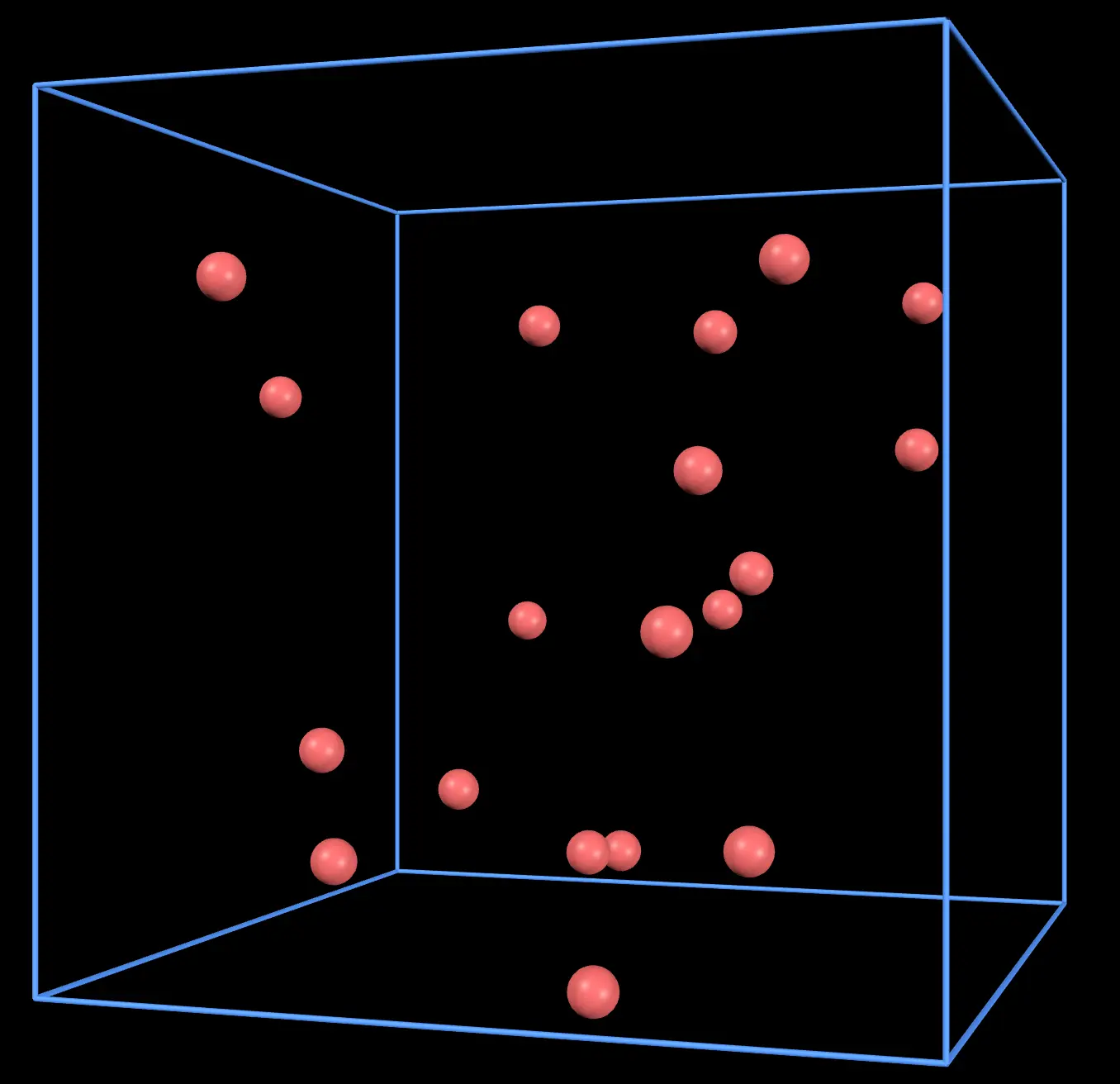
First, let's change the volume. Move the slider to reduce the side length, and you'll notice this:

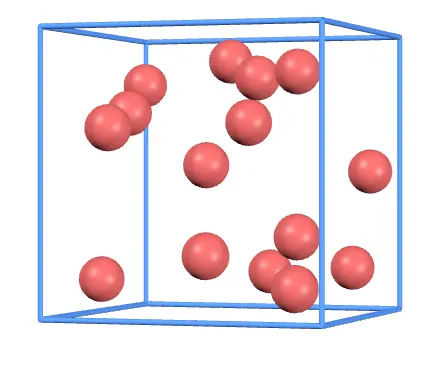
With a smaller container, gas molecules collide with the walls more frequently. This increases the force on the walls, resulting in higher gas pressure.

Next, let's increase the number of molecules. Restore the container size and press the Add button a few times. The number of molecules should now look like this:

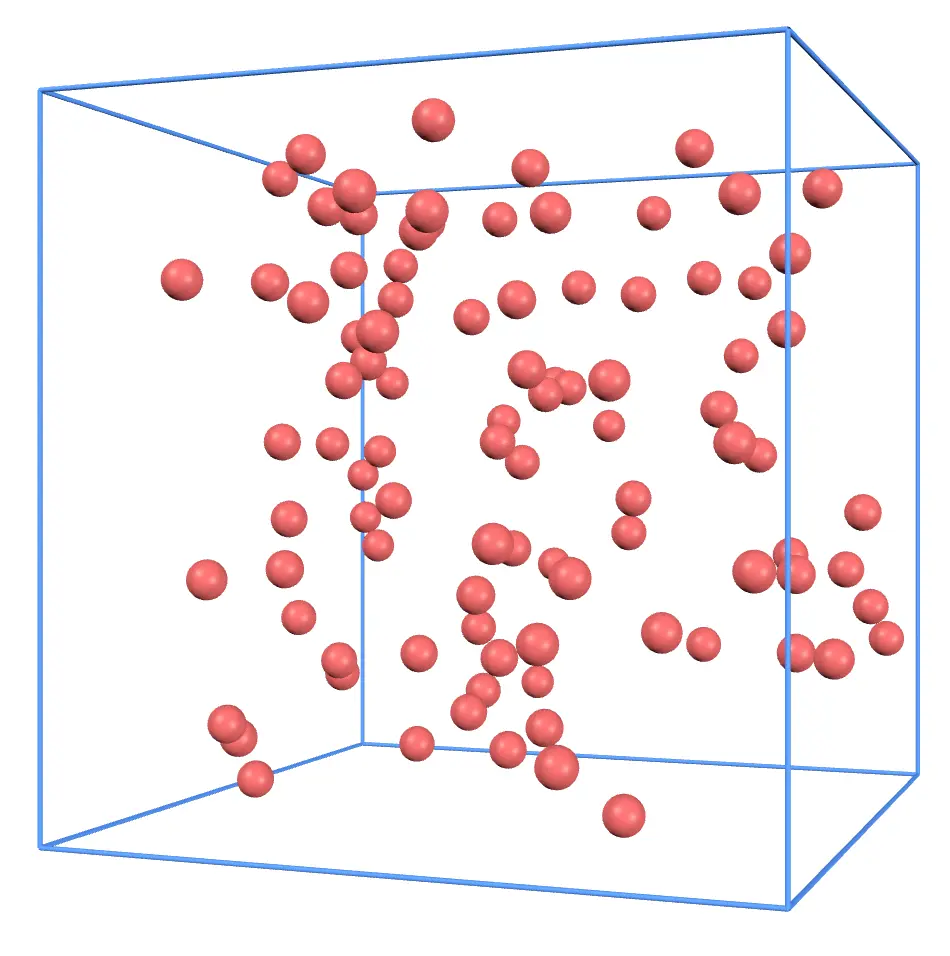
With more molecules, collisions with the walls become more frequent. This increases the force on the walls, raising the gas pressure.

Similarly, try increasing the speed of the gas molecules. As the particles move faster, they exert more force on the walls, leading to higher gas pressure.

Relationship with Temperature

How does gas pressure relate to temperature?

For an ideal gas, the following equation of state applies:

Here, $n$ is the number of moles of gas, and $T$ is the temperature of the gas. Substituting the earlier $p$ into this equation gives:

Using Avogadro's number $N_A$ , we have $N=nN_A$ . Simplifying gives:

Using the Boltzmann constant $k=\dfrac{R}{N_A}$ , we get:

This equation holds true.

The left-hand side represents the kinetic energy of gas molecules, while the right-hand side is proportional to the temperature $T$ . In other words, the kinetic energy of gas molecules is directly proportional to the gas's temperature!

This elegant conclusion, derived from the kinetic theory of gases, connects macroscopic properties like $p,\,T$ with microscopic properties like $m,\,v$through a simple equation.