Let's start by reviewing what we've covered so far! The key ideas in electromagnetism are:

These are the two main points. This time, we'll focus on electric fields!

Summary of Basic Laws

To summarize, the fundamental laws of electromagnetism can be captured in this table:

The goal is to understand this table!

While the lower part will be explained later, this time, we will focus on understanding that charges generate electric fields and electric fields exert force on charges.

Charges Generate Electric Fields

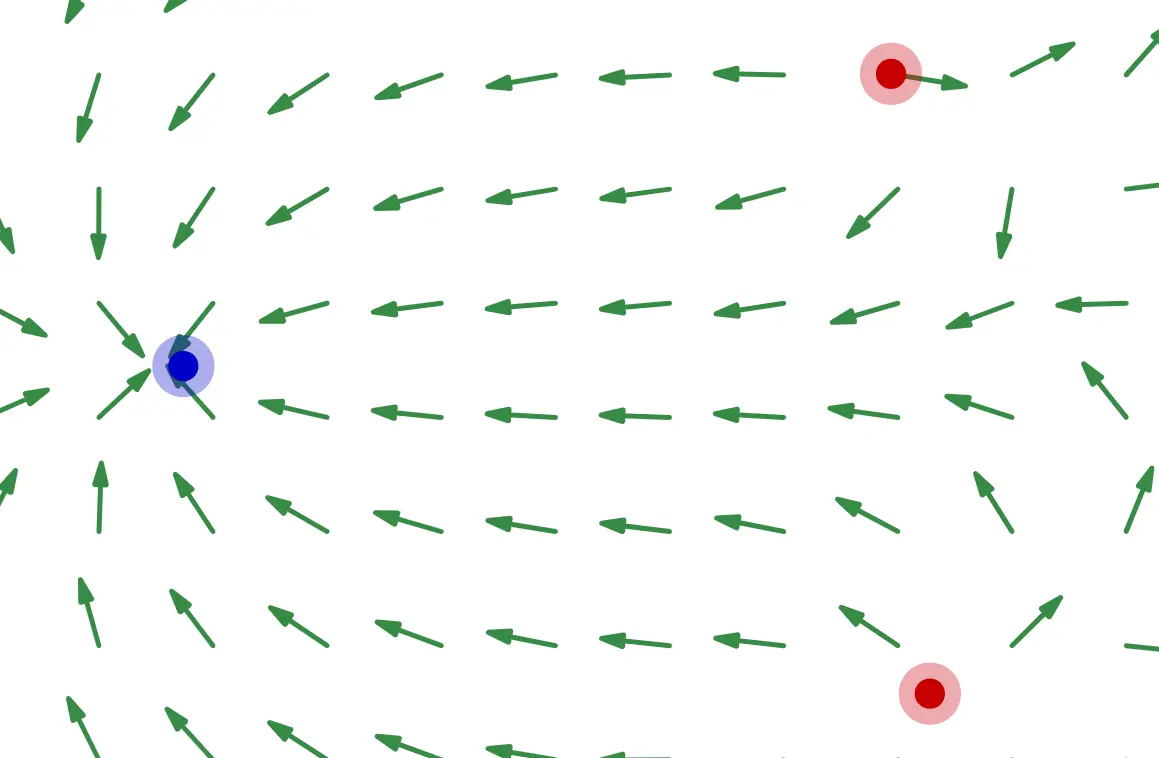
Charges create radial electric fields in the surrounding space just by existing.

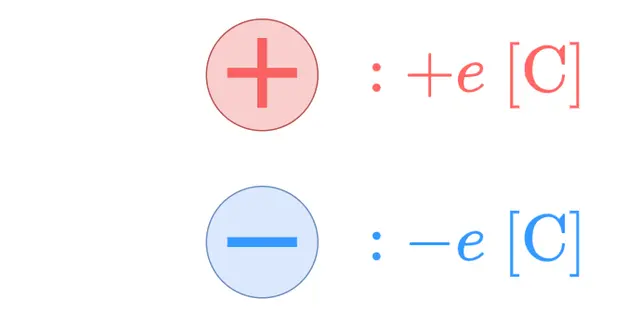
As shown in the diagram above, positive charges create outward electric fields, while negative charges create inward electric fields.

The magnitude of the electric field depends on the magnitude of the charge and the distance from the charge. Let the charge be $q\,[\mathrm{C}]$ and the distance be $r\,[\mathrm{m}]$. Then, the magnitude of the electric field $E$ is:

Here, $k$ is a constant called the Coulomb constant. (The unit of the electric field will be explained later.)

From this equation, we can see that the magnitude of the electric field is proportional to the magnitude of the charge and inversely proportional to the square of the distance.

Play with the Graph

Now, let's observe the electric field when three charges are placed!

You can drag the charges to move them. Also, you can adjust the values of the charges using the sliders below.

(For better visibility, the magnitude of the electric field is unified. In the graph linked below, you can switch to arrows that also consider magnitude.)

Did you get a sense of how electric fields are generated? Next, let's see how electric fields exert force on charges!

Electric Fields Exert Force on Charges

Electric fields exert force on charges at their location!

As shown in the diagram above, positive charges experience force in the same direction as the electric field, while negative charges experience force in the opposite direction!

The magnitude of the force is proportional to the magnitude of the electric field and the charge. Let the magnitude of the electric field be $E\,[\mathrm{N/C}]$ and the magnitude of the charge be $q\,[\mathrm{C}]$. Then, the magnitude of the force is:

Including direction, it can be expressed as:

Note that the direction of the force reverses when the sign of the charge changes!

This explains the unit of the electric field mentioned earlier.

The electric field represents the force experienced by a charge of $1\,\mathrm{C}$, so its unit is $\mathrm{N/C}$!

Interaction Between Charges

Combining these, we can see that charges indirectly exert force on other charges!

When a charge $q_1$ exists at a certain location, it creates a radial electric field $E=k\dfrac{|q_1|}{r^2}$ around it. If another charge $q_2$ is nearby, it experiences a force $F=|q_1|E=k\dfrac{|q_1q_2|}{r^2}$ due to the electric field at that location!

This force is called the Coulomb force.

Considering how the direction of the electric field and force changes with the sign of the charges, we can see that charges with the same sign repel each other and charges with opposite signs attract each other!

Summary

Here is what we learned this time:

Next time, let's explore the properties of magnetic fields!