Did you know that when two waves with similar frequencies overlap, a phenomenon called beats occurs? Let's explore, listen to, and experiment with beats today!

Listen to Beats

If you're using an iPhone or a similar device and can't hear the sound, make sure your device is unmuted and then press the Play/Stop button.

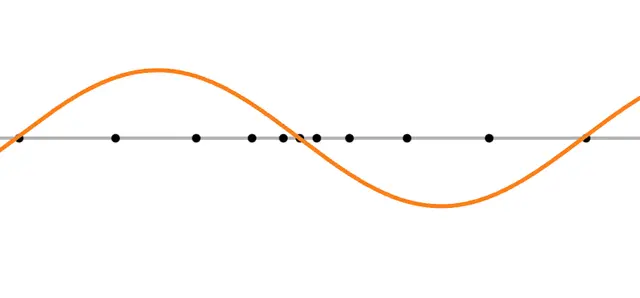
The two waves above represent two overlapping waves. The purple wave below shows the combined wave (the sound you actually hear).

Imagine standing at the position of the vibrating black dot. The vibration of the black dot represents the air vibrations that your ears perceive as sound.

What are Beats?

As mentioned earlier, beats are a physical phenomenon that occurs when two waves with close frequencies overlap.

The most striking feature of beats is their shape.

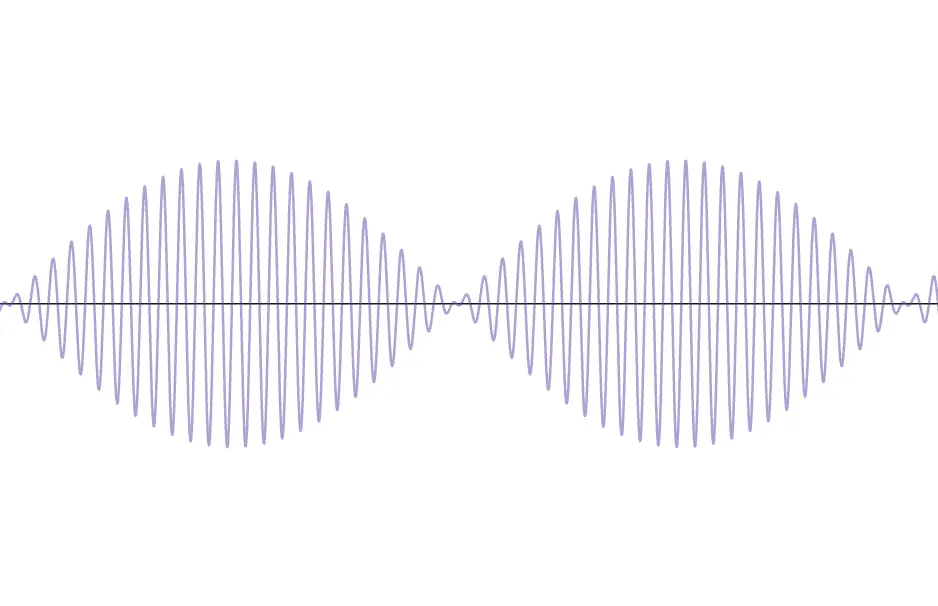
As shown in the figure, when two sine waves with close frequencies overlap, they form a wave that appears to have several lumps. More precisely, the amplitude of the wave changes periodically.

The louder the sound, the greater the amplitude. Since the amplitude of beats changes periodically, the volume also changes periodically.

This creates the characteristic "wah-wah-wah" sound you hear.

Deriving the Formula

Let's use calculations to understand why this phenomenon occurs!

First, the displacement of a sine wave with a frequency of $f\ [\mathrm{Hz}]$ and a speed of $v\ [\mathrm{m/s}]$ can be expressed as:

Now, consider two waves with frequencies $f_1,f_2\ [\mathrm{Hz}]$:

Let's consider their superposition. Since the two frequencies are close, $f_1\fallingdotseq f_2$ holds.

If we write the combined wave as $y_{\textrm{c}}(x,t)\ [\mathrm{m}]$, then:

The resulting formula looks complex...

Observing the final formula, you can see that it is the product of two waves.

The Wave Determining the Pitch

First, let's consider the first wave:

This represents a wave with a frequency of $\dfrac{f_1+f_2}2\ [\mathrm{Hz}]$. In other words, it corresponds to the average frequency of the two overlapping waves.

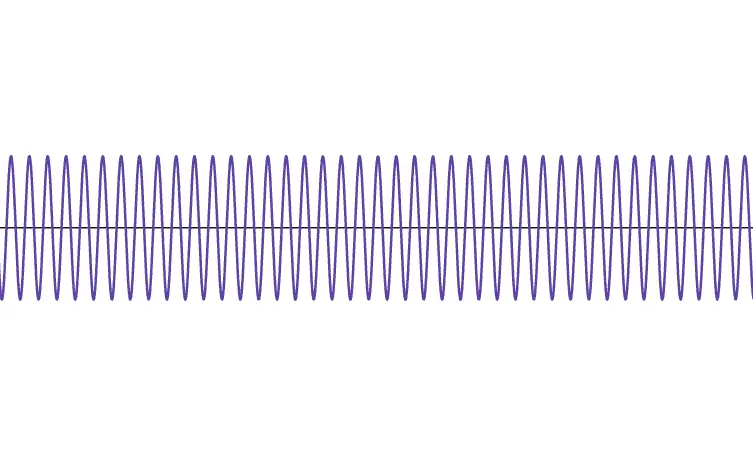
The Wave Representing Beats

The second wave is crucial:

This represents a wave with a frequency of $\dfrac{|f_1-f_2|}2\ [\mathrm{Hz}]$.

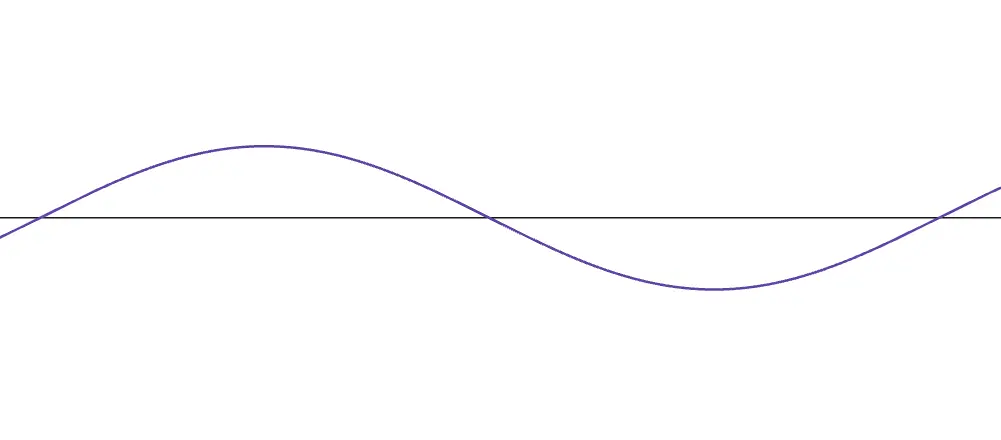
Considering $f_1\fallingdotseq f_2$, this frequency is very small. In other words, the wavelength becomes very large, as shown in the figure.

The Product of Two Waves

What happens when these two waves are multiplied?

If you multiply the two waves as they are, the resulting wave looks like this:

Notice that the envelope of the wave corresponds to the shape of the second wave with a large wavelength (strictly speaking, twice its amplitude).

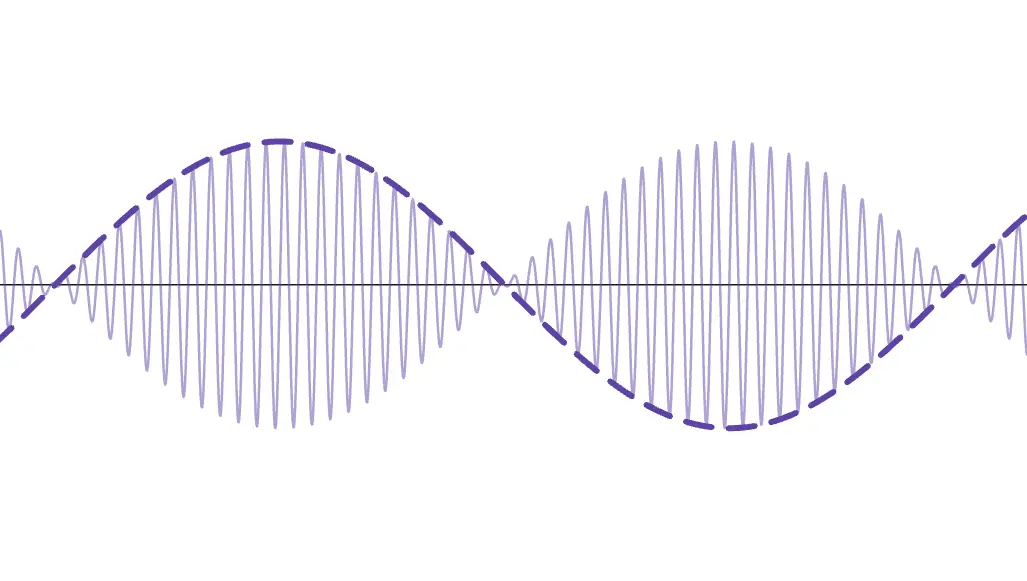
In other words, the periodic change in the amplitude of the wave due to the second wave with a large wavelength results in beats!

The Frequency of Beats

Let's determine the frequency of beats.

The frequency of beats refers to how many times the volume (amplitude) oscillates per second. In other words, how many "wah-wah" sounds occur per second.

Focus on the second wave:

As mentioned earlier, this wave has a frequency of $\dfrac{|f_1-f_2|}2\ [\mathrm{Hz}]$, but this is not the frequency of beats.

Each time this wave oscillates once, the beats oscillate twice! Therefore:

is the frequency of beats!

Beats in Everyday Life

A common example of beats in everyday life is the dissonance in piano chords.

When you play two adjacent notes (e.g., B and C) on a piano simultaneously, a dissonant sound occurs. This can be attributed to beats caused by the close frequencies of the adjacent notes.

For more details, check out the following article!

Understanding Chords and Waves: Harmony and Dissonance