皆さんは普段音楽を聴いていて、綺麗で安定した和音と汚く不安定な和音が存在することに気づいたことはありますか？

今回は波の振動数による音の違いや、それぞれの和音の波がどのような形をしているかを調べてみましょう！

以下、C, D, E, F, G, A, B はそれぞれ ド, レ, ミ, ファ, ソ, ラ, シ と同じです。

音を鳴らしてみよう

上側のグラフは実際に聞こえる音波（合成波）、下側のグラフはそれぞれの音の音波を重ねて表示しています。

(iPhone やiPadでこのページを見ている人は、音が出ない場合はミュートを解除して下さい)

ピアノの鍵盤をクリックするかグラフの右下のボタンをクリックして、それぞれの和音がどのような波の形をしているか観察してみましょう。その後に再生ボタンを押して、その和音がどのような音なのか聴いてみましょう。

（音割れ防止のため、再生中に新たに追加した音はすでに鳴っている音より小さい音量となります。構成音を均一な音量で聴きたい場合は、一度再生を止めてから再生し直してください。）

グラフ右下の「Cメジャー」などという言葉はコードといって、和音の名称です。ここには主要な和音6つを並べました。それぞれの特徴は後に説明します。

グラフ右上のボタンでは、音律を純正律と平均律で選択することができます。音律とは、それぞれの音の周波数がいくつなのかを基準の周波数をもとに定めるものです。後に詳しく解説します。

音の周波数はどうやって決める？

音は周波数が変わると高さが変わるのはご存じの方が多いと思いますが、どのようにその周波数を決めるのかはご存知ですか？

まず、基準となる音とその周波数を決めます。よく用いられるのは中央の A（ラ）を 440 Hz とするものです。

その後、それ以外の音の周波数と元となる周波数との比率を決め、それをもとに全て音の周波数を決定します。この比率の規定を音律と言います。

よく用いられる音律は以下の通りです。

平均律

平均律は数学的にきれいに作られた、現代では主流となっている音律です。

最も大きな特徴は、隣り合う音同士の周波数比が一定、つまり周波数が等比数列になっている点です。

まず、オクターブの周波数比を2倍になるようにします。そして、それに合うように隣り合う音の周波数比を決めます。

つまり、隣同士の周波数比は $\sqrt[12]{2}$ となります。

ある C（ド）を基準とした1オクターブ分の周波数比は次のようになります。

純正律

平均律は一見綺麗に定義されて使い勝手も良さそうですが、周波数比が汚い無理数になっていることで、和音の響きがイマイチになってしまうことがあります。

そこで、周波数比が平均率の周波数比に近い有理数の値になるように、少しずつずらして調整したのが純正律です。（周波数比が有理数のほうが響きが綺麗になる理由は後ほど説明します）

あるCを基準とした1オクターブ分の周波数比は次のようになります。

一見上手く作られた音律のように見えますが、どの音階（スケール）を基準にするかでそれぞれの音の周波数が変わってしまうという性質があり、転調・移調が困難であるという欠点があります。

例えば、曲の途中でドレミファソラシド（Cメジャースケール）からレミファ#ソラシド#レ（Dメジャースケール）に転調しようとすると、もともとは純正律であったとしても、転調したあとは純正律にはなりません。

安定な和音と不安定な和音

では、どのような波がどのような音になるのでしょうか？

以下、波の特徴がわかりやすい純正律で行ってください。

まずグラフ下の「オクターブ」と書かれたボタンを押してから再生ボタンを押して音を聴いてみてください。
グラフは見やすいように適宜拡大縮小しましょう。

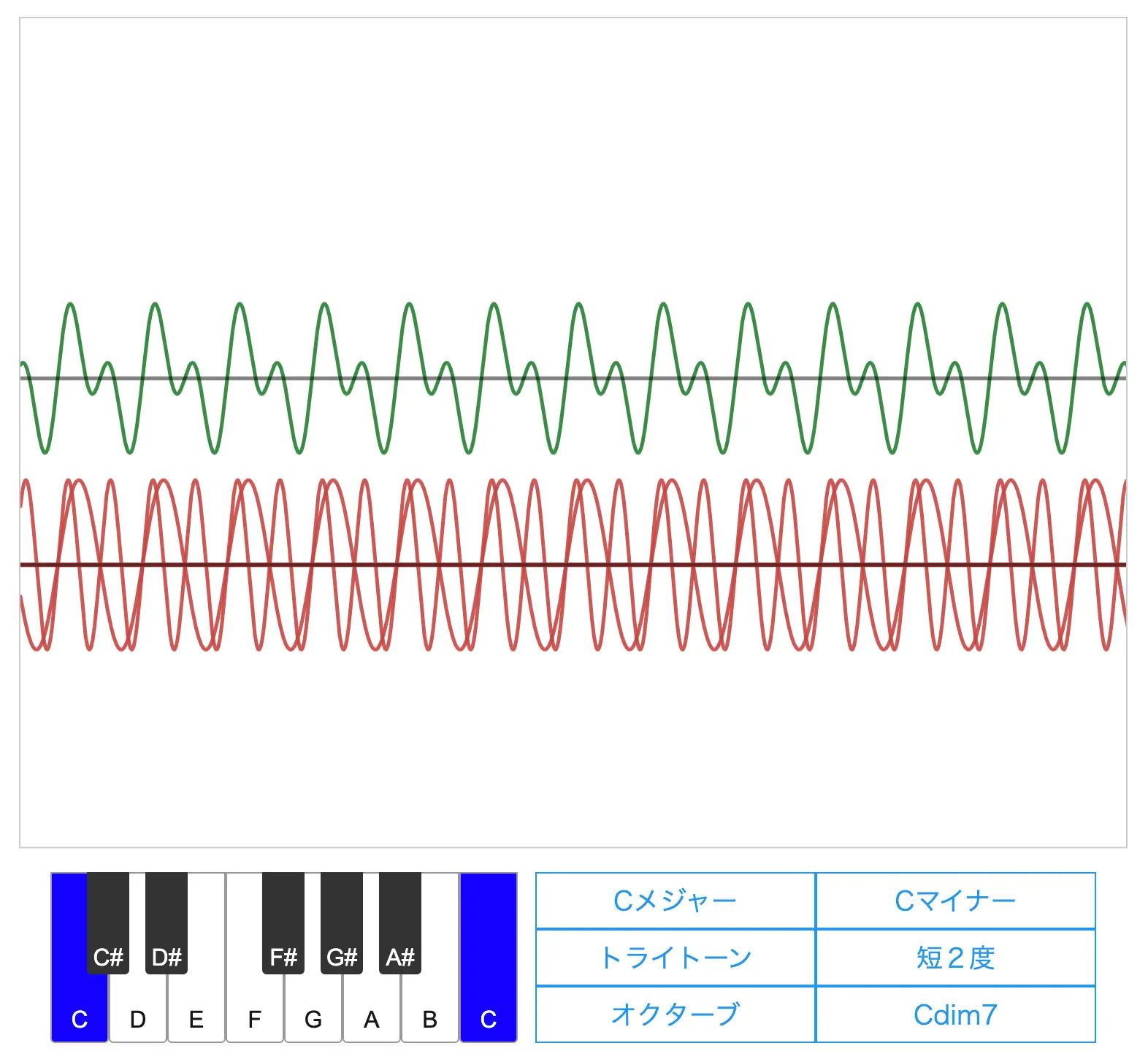
とても安定した音になったと思います

次に「トライトーン」と書かれたボタンを押して音を聴いてみてください。

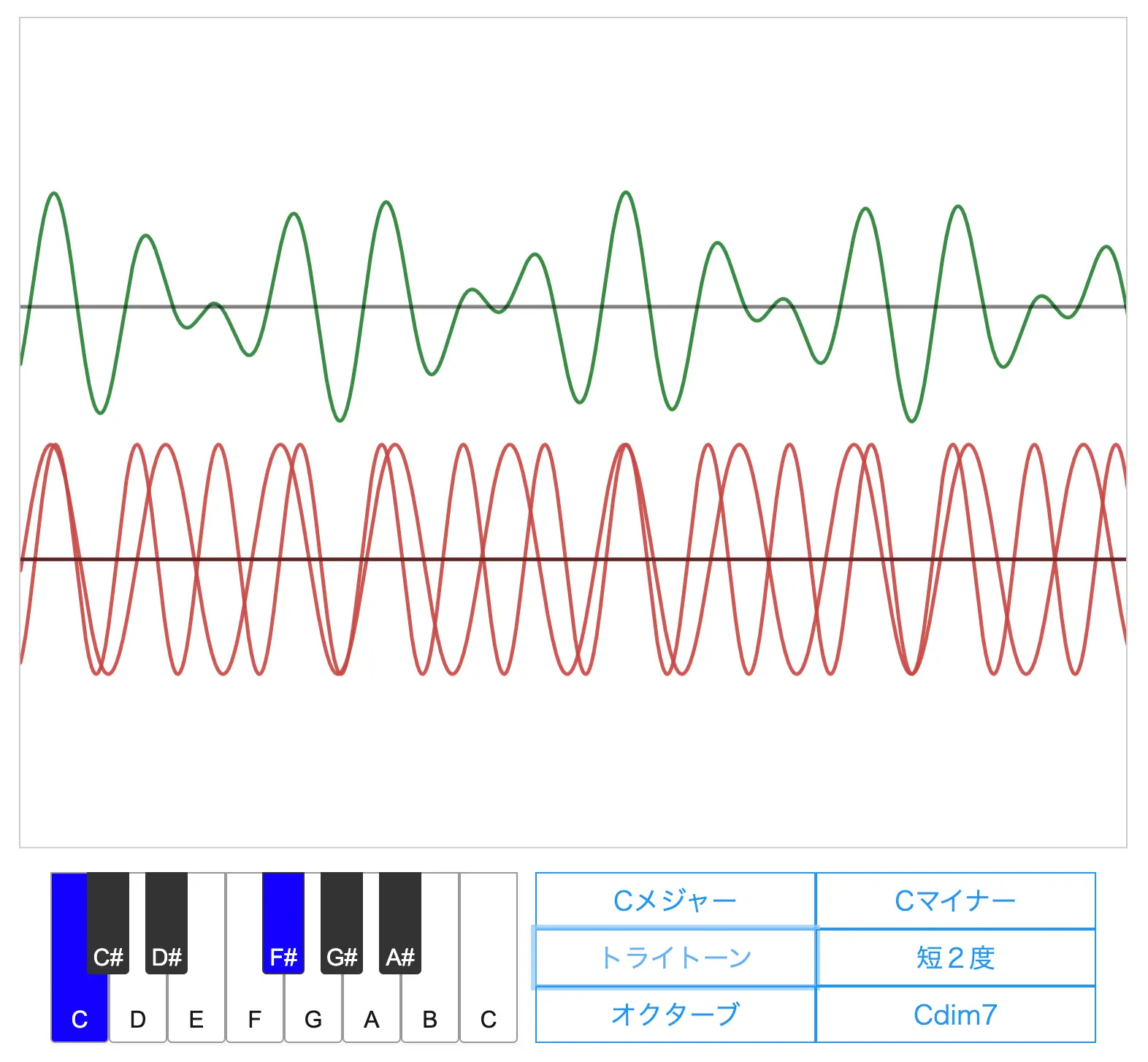
とても不安定な音になったと思います。

最後に「短2度」と書かれたボタンを押して音を聴いてみてください。

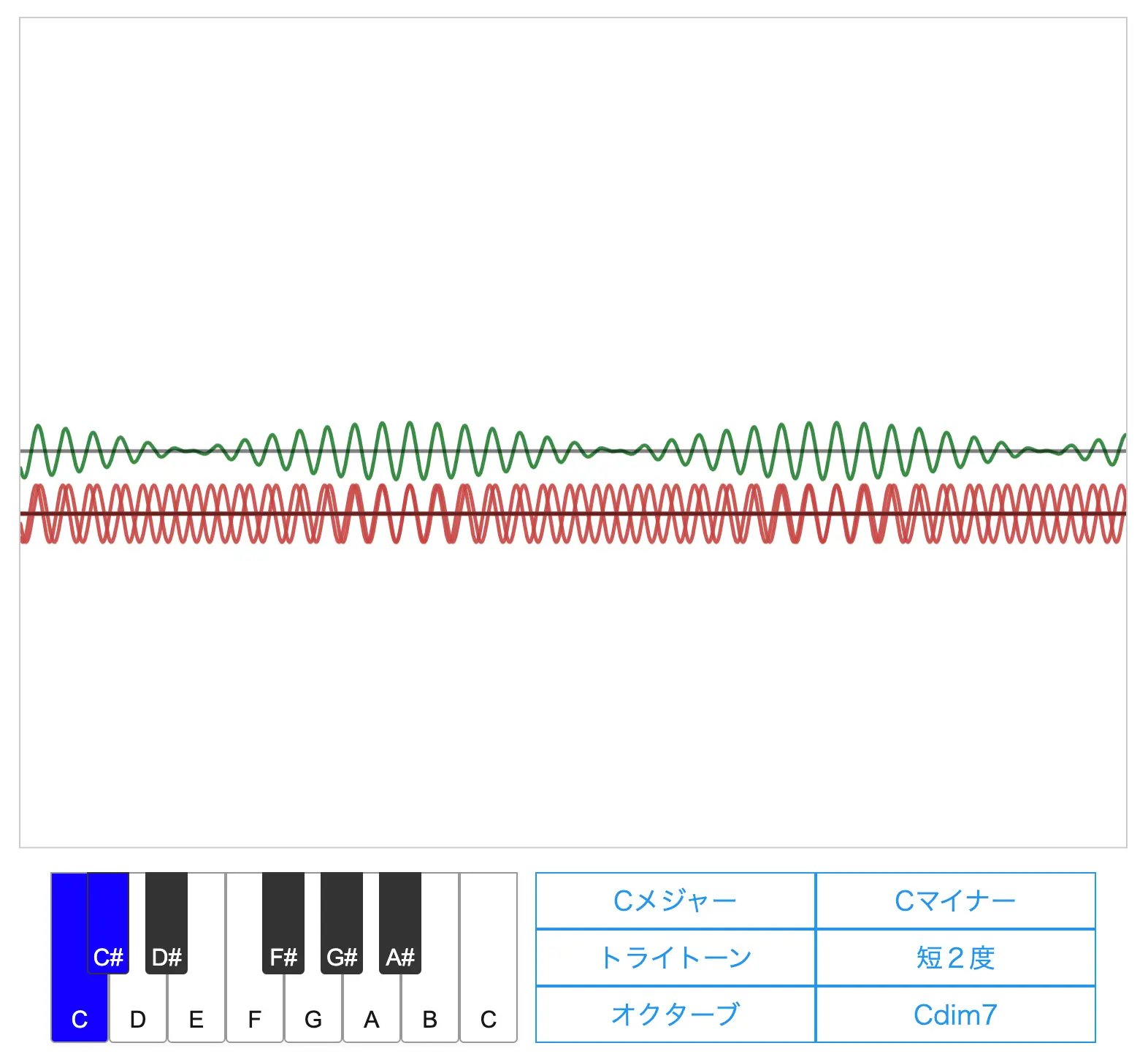
こちらもとても不安定な音になり、うなりも聞こえると思います。（よく不協和音と言われる音です）

このように異なった特徴をもつ音になる理由は3つの波の形を見るとわかります。

オクターブにおいては、2つのC（ド）の周波数比が 1 : 2 と簡単な整数比であるために、合成波は短い周期で同じ形の波が繰りかえされます。

対してトライトーンや短2度においては、2つの音の周波数比が 32 : 45 や 15 : 16 と複雑になってしまうため、合成波はなかなか同じ形の波が現れない複雑な形となってしまいます。

さらに短2度においては2つの音が隣接していて周波数が近いため、うなりも聞こえます。

他の例を見てみましょう。

「Cメジャー」「Cマイナー」「Cdim7ディミニッシュ・セブンス」についても同様に音を聞いてみてください

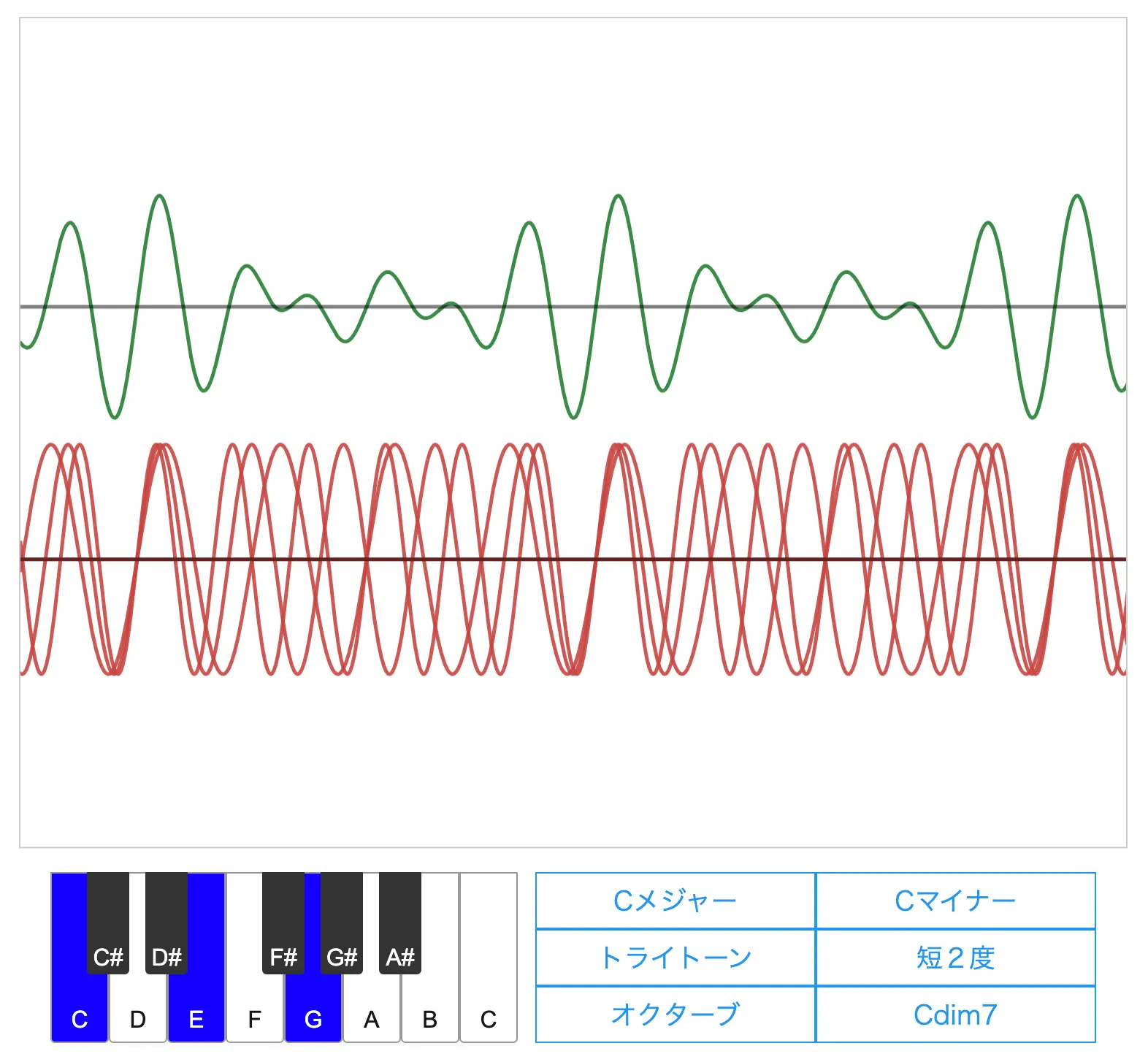
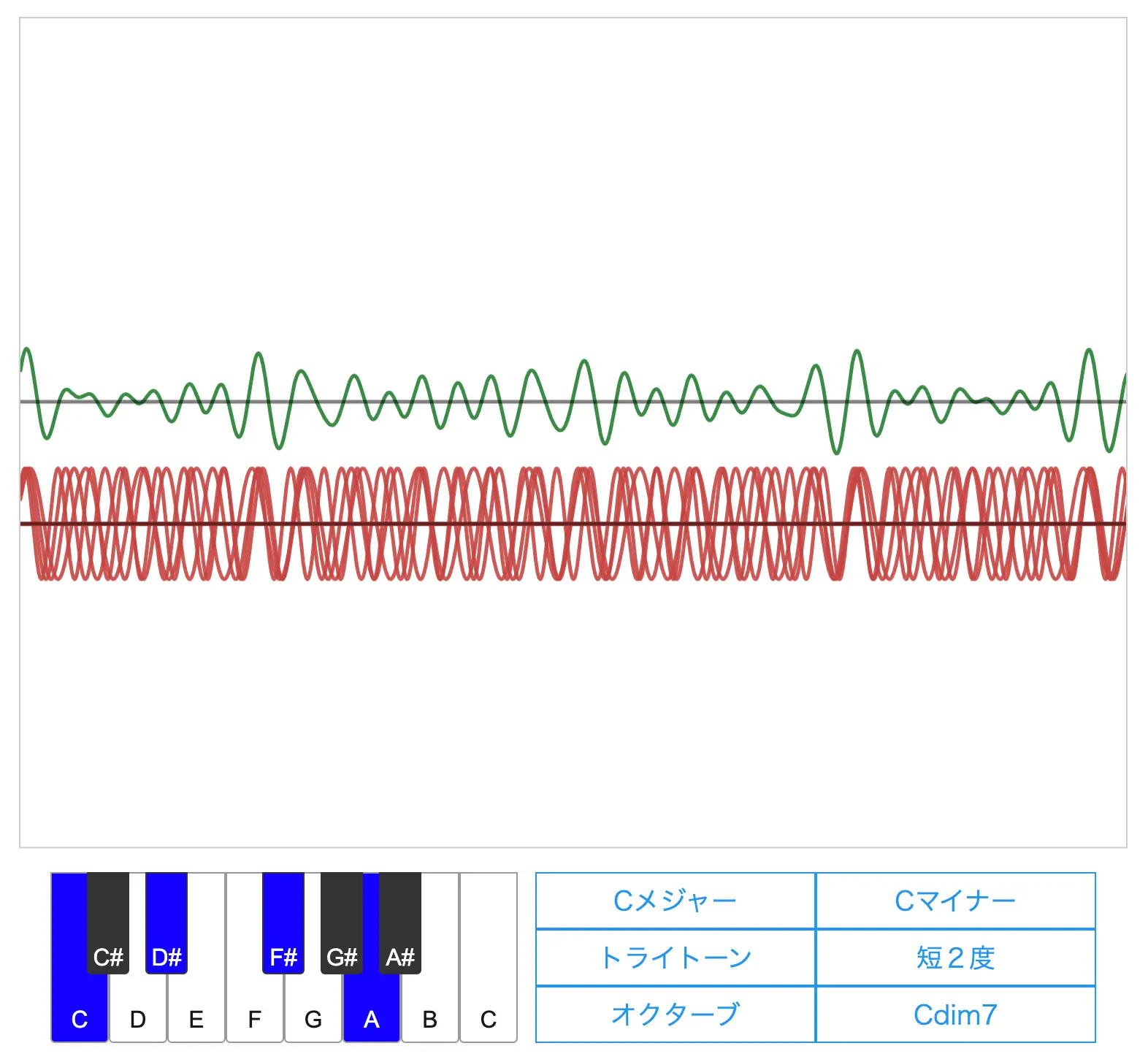
Cメジャーはとても安定した音になりますが、CマイナーとCdim7は不安定な音になると思います。

Cメジャーの周波数比は 4 : 5 : 6（有名な比なので知っていて損はないです）
Cマイナーの周波数比は 10 : 12 : 15
Cdim7の周波数比は 480 : 576 : 675 : 800

であるので、Cメジャーの周波数比はとても簡単であることがわかると思います。
（CマイナーもCdim7に比べれば簡単な周波数比であるので、暗い音ではありながらも、Cdim7の張りつめた不安定な音にくらべたら安定な音であると言えます。）

また、Cdim7には先ほど出てきたトライトーンが2組入っています（C,F#とD#,A）。これもCdim7がとても不安定になる証拠の一つです。

つまりまとめると、構成音の周波数比が簡単な整数比であり、合成音の周期が短いほど安定な音に聞こえるということです。