皆さんは2つの水面波が干渉した姿を見たことがありますか？今回は、水面波の干渉をアニメーションで見てみましょう！

アニメーション

デフォルトでは合成波（実際に観測できる波）が表示されています。まずは、合成波と書かれたスイッチをオフにして、代わりに波1と書かれたスイッチを入れてみてください。

図のようなオレンジ色の水面波が表示されたはずです。次に波1というスイッチを切って、波2のスイッチを入れてみてください。

図のように、中心（波源）が先ほどとずれた緑色の水面波が表示されたはずです。

これら２つの波を干渉させた（重ね合わせた）波が、最初に表示されていた合成波です。今回はこの合成波について考察していきましょう！（腹線・節線については後ほど解説します）

合成波の特徴

では、合成波の特徴を見ていきましょう！大まかに以下の特徴があります。

腹線・節線とは

水面波を合成すると、振幅が最大の点や振幅が０の点が線上にできます。それらの線を、腹線・節線と言います。

これは、合成波を上から見た図です。何やら線が見えませんか？

腹線・節線と書かれたスイッチを入れると、腹線・節線を可視化することができます。このようになります。

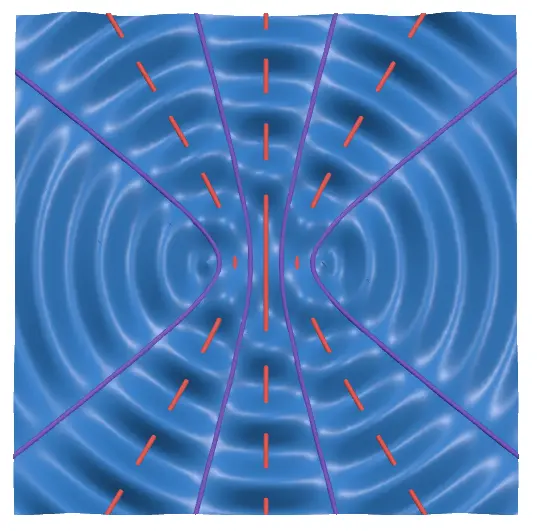
赤い線が腹線、紫の線が節線を表しています。

振幅を大きくして横から見てみると分かりやすいですが、たしかに腹線上の点は振幅が最大となっていて、節線上の点は振幅が０となっていることが分かります。

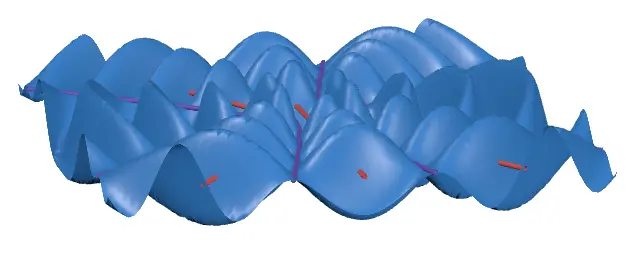
これらは、波源が同位相の時を表しています。つまり、２つの波の波源は全く同じように振動しているということです。

では、逆位相と書かれたスイッチを入れてみましょう。２つの波の波源が逆向きに振動を始めます。

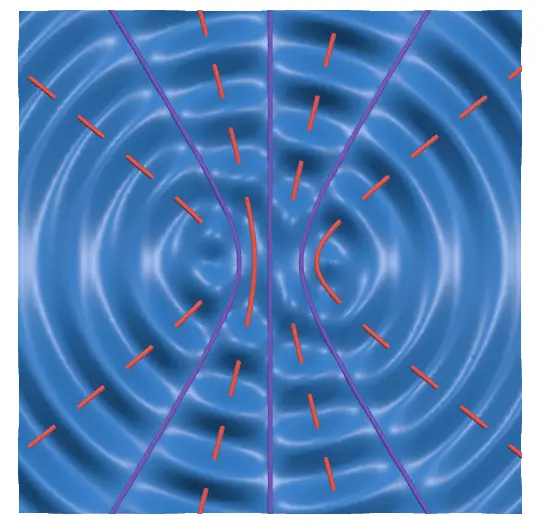
この時、図のように腹線と節線が互いに入れ替わっていることが分かります。

腹線・節線の位置

ある点の振幅が腹や節になるかどうかは、その点から波源までの距離を考えるとわかります。２つの波源までの距離の差を経路差と言います。

これは、今回の水面波に限らず、任意の波の干渉において応用できる考え方です。

経路差を考えると、腹線・節線の位置を求めることができます。

波源の位置を $(p,0),(-p,0)$ とすると、点 $(x,y)$ における経路差は

となります。これに対して先ほどの考え方を使うと、腹線や節線の具体的な式を求めることができますが、複雑なので割愛します。

しかし、腹線や節線が双曲線の形をすることは簡単にわかります。

腹線や節線は経路差が一定の点を結んだ線です。つまり、波源からの距離の差が一定である点を結んだ線になります。

これは双曲線の定義になっています！（厳密には直線となる場合もあります）