UNS物理
最も遠くに飛ばせる角度は？放物運動で遊ぼう
parabolicmotion
作成日：2025/3/16

皆さんは、放射角度が何度の時に最も遠くに物体を飛ばせるか知っていますか？シミュレーションで実際に試してみましょう！

最後に空気抵抗がある場合についても考察します。

放物運動のシミュレーション

放射角
初速
Desmos のグラフはこちら
グラフのみを表示

放射角をいじってみて、何度の時に最も遠くまで飛ばせるかを調べてみましょう！

START/STOP ボタンを押してから放射角をいじると、45∘45^\circ の時に最も遠くまで飛ばせることがわかると思います！

計算してみよう

では、実際に到達する距離を計算してみましょう！

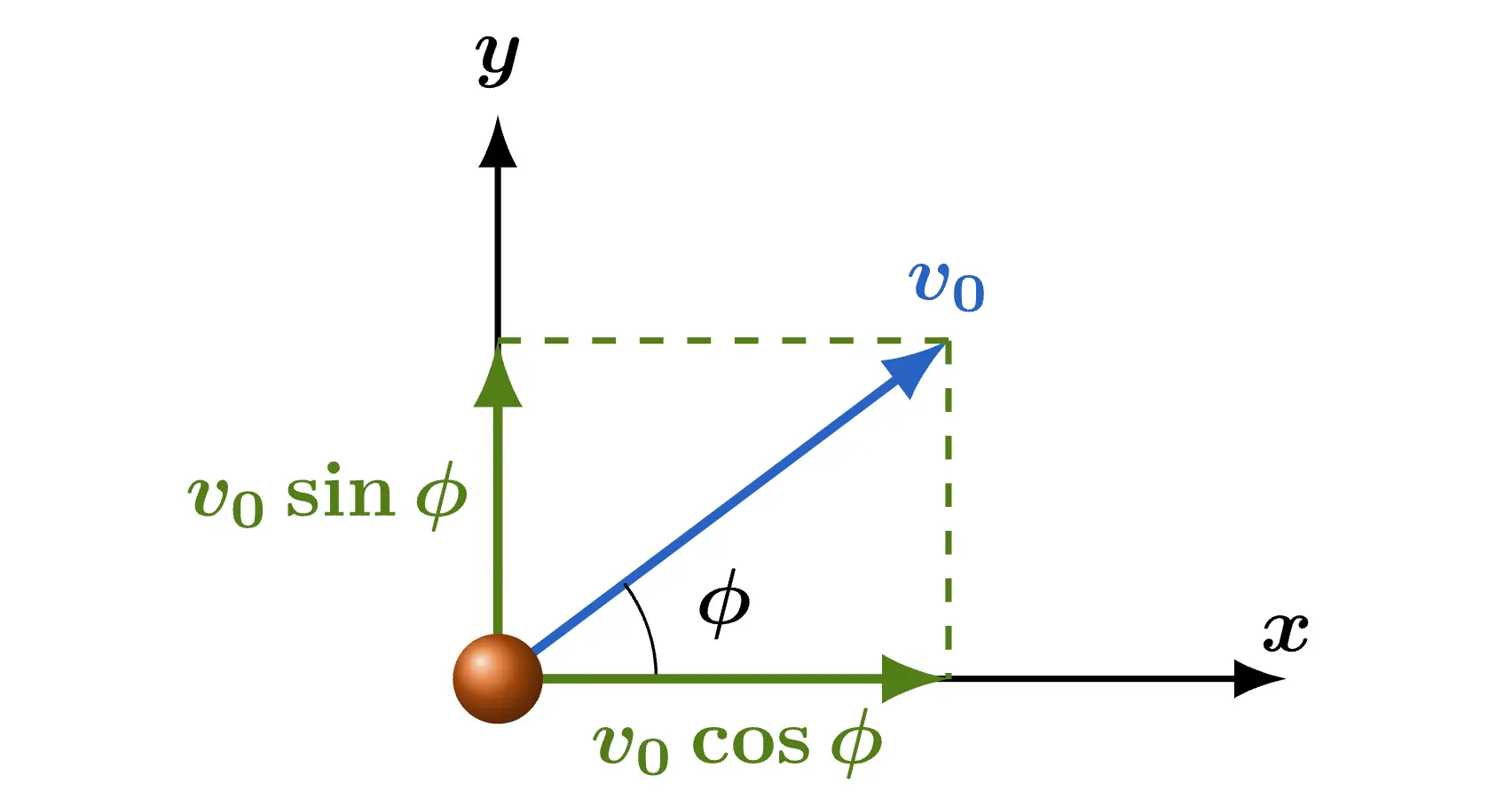
放射角を ϕ\phi 、初速を v0v_0 でボールを投げることを考えます。ただし、重力加速度を gg とします。

この時、yy 軸方向にはボールは初速度が v0sin⁡ϕv_0\sin \phi の等加速度運動をします。よって、時刻 tt での位置は

ay(t)=−g∴ vy(t)=v0sin⁡ϕ+∫0tay(t)dt=v0sin⁡ϕ−gt∴ y(t)=∫0tvy(t)dt=(v0sin⁡ϕ)t−12gt2 \begin{align*} a_y(t)&=-g\\ \therefore\ v_y(t)&=v_0\sin\phi +\int_0^ta_y(t)dt=v_0\sin\phi-gt\\ \therefore\ y(t)&=\int_0^tv_y(t)dt=(v_0\sin\phi )t-\frac12gt^2 \end{align*}

となります。よって、地面に落ちた時の時刻 t1t_1 は、

y(t1)=0∴ t1=2v0sin⁡ϕg (≠0)y(t_1)=0\quad\therefore\ t_1=\frac{2v_0\sin\phi}g\ (\neq 0)

と求まります！

xx 軸方向には速度 v0cos⁡ϕv_0\cos\phi の等速直線運動をするので、時刻 t1t_1 での位置、つまり到達距離 LL は

L=(v0cos⁡ϕ)t1=2v02sin⁡ϕcos⁡ϕg=v02sin⁡2ϕgL=(v_0\cos\phi)t_1=\frac{2v_0^2\sin\phi\cos\phi}g=\frac{v_0^2\sin2\phi}g

と求まります。

よって、到達距離 LL が最大となる ϕ(0<ϕ<π2)\phi\left(0<\phi<\dfrac{\pi}2\right) は、sin⁡ϕ=1\sin\phi=1 となる時より、ϕ=π4\phi=\dfrac{\pi}{4} となります！

空気抵抗がある場合（発展）

空気抵抗がある場合の放物運動はどのようになるでしょうか？

空気抵抗を厳密に記述することは難しいですが、大まかに速度の大きさに比例する粘性抵抗と、速度の大きさの2乗に比例する慣性抵抗があります。

今回は、粘性抵抗のみが働く状況を考えてみましょう。比例定数を kk とすると、抵抗力は速度と逆向きに k∣v→∣k|\overrightarrow v| となるので、運動方程式は

mdvxdt=−kvxmdvydt=−kvy−mg \begin{align*} m\frac{dv_x}{dt}&=-kv_x\\[8px] m\frac{dv_y}{dt}&=-kv_y-mg\\ \end{align*}

となります。

１つ目の式を解くと、

dvxdt=−kmvx∴ vx=C0e−(k/m)t\frac{dv_x}{dt}=-\frac km v_x\quad\therefore\ v_x=C_0e^{-(k/m)t}

vx(0)=v0cos⁡ϕv_x(0)=v_0\cos\phi であるので、C0=v0cos⁡ϕC_0=v_0\cos\phi です。よって、

vx=(v0cos⁡ϕ)e−(k/m)tx=∫0tvxdt=mv0cos⁡ϕk(1−e−(k/m)t)\begin{align*} v_x&=(v_0\cos\phi)e^{-(k/m)t}\\[5px] x&=\int_0^tv_xdt=\frac{mv_0\cos\phi}{k}(1-e^{-(k/m)t}) \end{align*}

と xx 座標が求まります。

2つ目の式を解くと、

dvydt=−km(vy+mgk)∴ vy+mgk=C1e−(k/m)t\begin{align*} \frac{dv_y}{dt}=-\frac km \left(v_y+\frac{mg}{k}\right)\\[10pt] \quad\therefore\ v_y+\frac{mg}{k}=C_1e^{-(k/m)t} \end{align*}

vy(0)=v0sin⁡ϕv_y(0)=v_0\sin\phi であるので、C1=v0sin⁡ϕC_1=v_0\sin\phi です。よって、

vy=(v0sin⁡ϕ)e−(k/m)t−mgky=∫0tvydt=mv0sin⁡ϕk(1−e−(k/m)t)−mgkt\begin{align*} v_y&=(v_0\sin\phi)e^{-(k/m)t}-\frac{mg}{k}\\[5px] y&=\int_0^tv_ydt=\frac{mv_0\sin\phi}{k}(1-e^{-(k/m)t})-\frac{mg}{k}t \end{align*}

と、yy 座標も求まります。

放物運動のシミュレーション（空気抵抗あり）

これをシミュレーションにすると、このようになります！

放射角
抵抗
Desmos のグラフはこちら
グラフのみを表示

抵抗力の大きさにもよりますが、45∘45^\circ よりも小さい放射角の時に、到達距離が最も大きくなったのではないでしょうか？

SHARE
<
monkey
モンキーハンティングで遊ぼう
billiardpi
衝突回数で円周率を求める？シミュレーションしてみよう
>
Images are created with the Desmos Graphing Calculator, used with permission from Desmos Studio PBC.
© 2024 UNS Physics. All Rights Reserved.