トムソンの実験や磁場偏向の実験によって、電子の質量と電荷の比である比電荷を求めることができます。今回は、これらの実験をアニメーションで見てみましょう！

アニメーション

実験の概要

この２つの実験でしていることは大まかには同じです。

まず、左から電子を発射します。その後、トムソンの実験では電場で、磁場偏向では磁場を用いて電子に力を与え、軌道を曲げていきます。そして、最終的に電子がたどり着いたスクリーン上の位置を計測するといった流れです。

この計測結果から電子の比電荷を導くことができます！ではそれぞれの実験を１つずつ見ていきましょう！

トムソンの実験

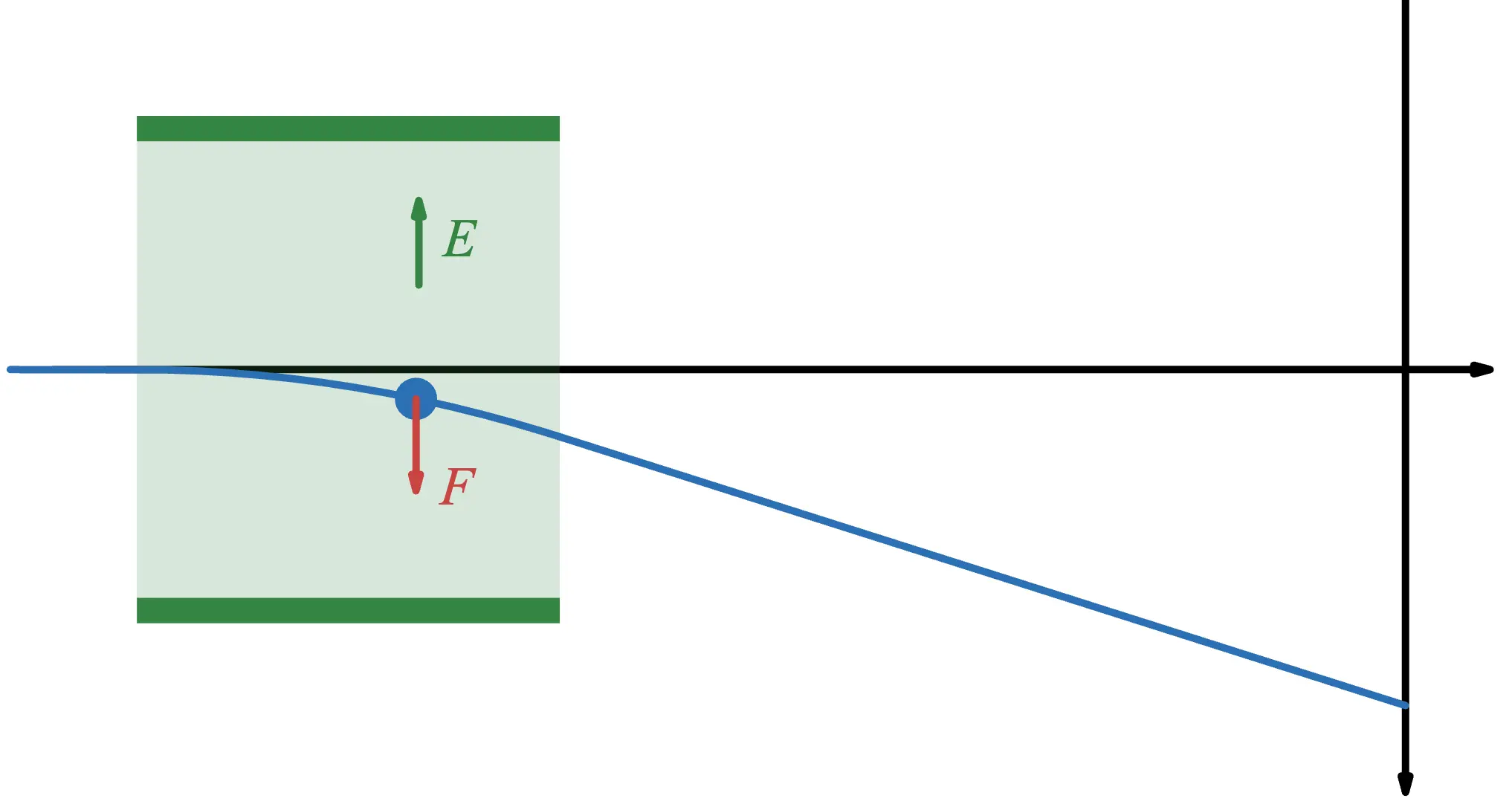
トムソンの実験では、電場を用いて電子に力を与えていきます。電位の違う金属板を用意すると、その間に一様電場が生まれます。この間に電子を通すという流れです。

濃い緑は金属板、薄い緑は電場が生じている箇所を表しています。コンデンサーをイメージしてもらえるとわかりやすいと思います。

電子は電場によって力を受けていきます。電子の電荷の符号は負なので、電場と逆向きに力を受けます。

ただし、電子に働く重力の大きさは非常に小さいので無視します。

このとき、力の向きは常に下向きなので、鉛直下方向を正とすると、運動方程式は

となります。ただし、電子の質量を $m$ 、電子の電荷を $-e$ 、下向きの加速度を $a$ 、電場の大きさを $E$ としました。

これより、

となります。つまり、電子は等加速度運動をするわけです。これは重力を下向きに受けているのと全く同じ状況なので、電子は放物線を描いて運動していきます。

電場ゾーンを抜けると、そこからは力を受けません。電子は等速度直線運動をしてスクリーンに到達します。

電場ゾーンの距離を $l$ 、初速度を $v_0$ とすると、電子が電場ゾーンにおいて鉛直方向に進む距離は

です。その後の力を受けない区間で鉛直方向に進む距離は、電子の鉛直方向の速度が $at=\dfrac{eE}{m}\dfrac l{v_0}$ であることから、

です。ただし、この区間の距離を $L$ としました。

よって到達するスクリーンの位置 $y_0$ は、これらを足して、

です。これを変形すると、

となり、比電荷 $e/m$ を計測結果から求めることができました！

磁場偏向の実験

磁場偏向の実験では、磁場を用いて電子の軌道を曲げていきます。以下のように、磁場がかかっている区間を作り、そこに電子を照射します。

電子は磁場からローレンツ力を受けます。先ほどと大きく違う点として、ローレンツ力の向きは電子の運動する向きと垂直です。電子はローレンツ力によって円運動を行い、その速さは一定です。

よって中心方向の運動方程式より、

が成立します。ただし、$r$ はこの円運動の半径です。ここで、以下のように角 $\theta$ を定めます。

すると図より、

が成立します。スクリーンの到達位置を $y_0$ とすると、

となります。$r\gg l$ であると仮定すると、$\theta\ll 1$ なので、

と近似することができます。これを用いると、

となります。これを変形すると、

となり、比電荷 $e/m$ を計測結果から求めることができました！

比電荷の意義

電子の質量や電荷はとても小さい値であり、測定することが難しいです。しかし、これらの実験によって電子の比電荷 $e/m$ を求めることができます。

20世紀になって、ミリカンは油滴を用いた実験によって電気素量 $e$ を求めることに成功します。これとすでに求められていた比電荷の値を用いることで、電子の質量 $m$ も求めることができたのです。