UNS物理
固定端・自由端反射のポイントを図で解説
jiyukotepoint
作成日：2025/3/10

正弦波の自由端反射・固定端反射において受験で問われやすいポイントを紹介します。

自由端反射・固定端反射って何？？という人はまずはこちらの記事を読みましょう！

jiyukotesee
【グラフで遊ぶ】固定端・自由端反射を見よう

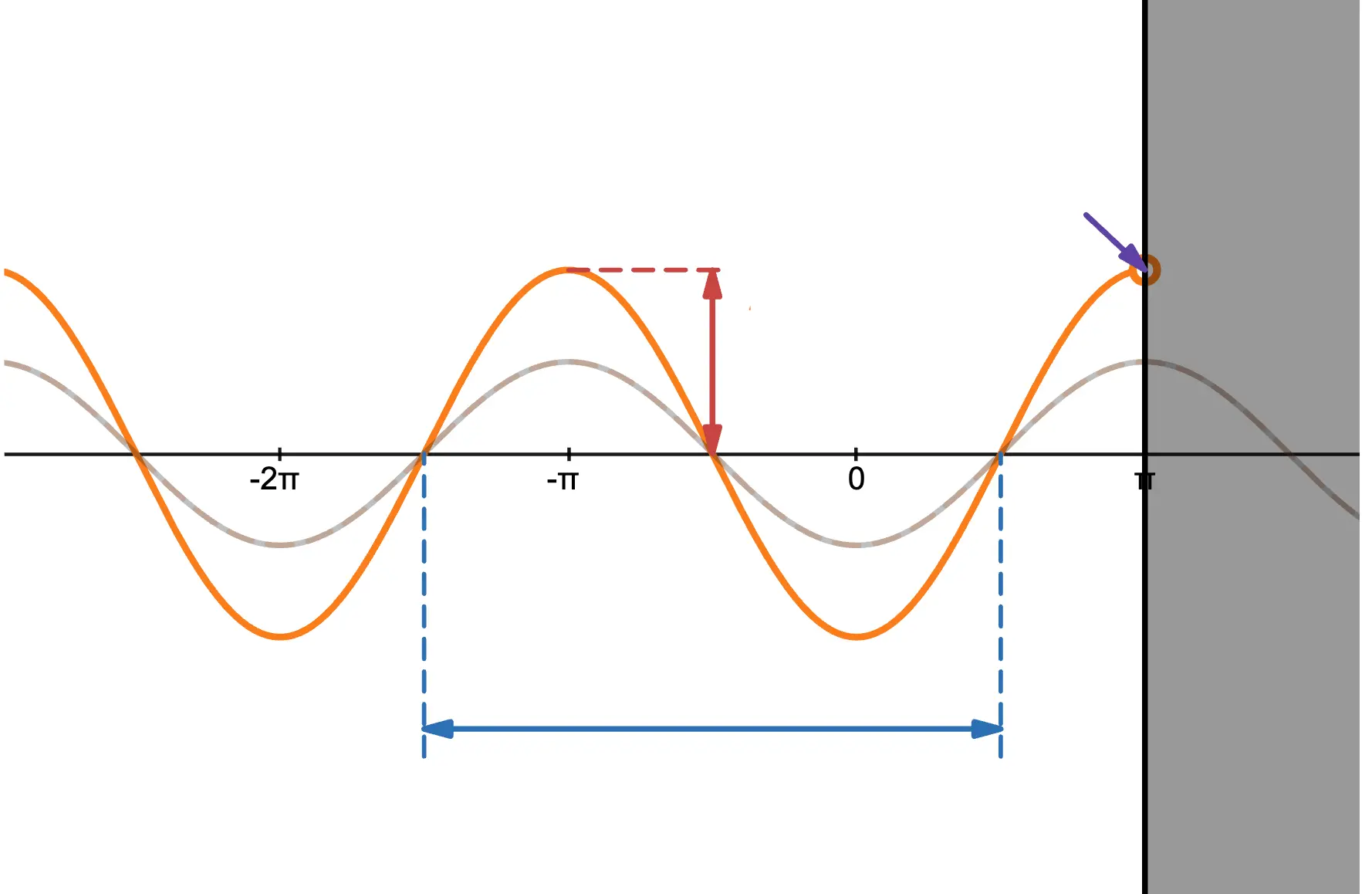
正弦波の反射のグラフ

前回の記事でも載せた正弦波の反射のグラフを再掲します！

波源

入射波

反射波

合成波

●

（点線）

（実線）

Desmos のグラフはこちら
グラフのみを表示

押さえておきたいポイントは以下です。

自由端反射・固定端反射のポイント

入射波が波長 λ\lambda 、振幅 AA の時

【波源 〜 反射板】

波長 λ\lambda 、振幅 2A2A の定常波（節・腹の位置に注意！）

【波源より先】

波長 λ\lambda の進行波（振幅は波源ー反射板の距離に依存）

それぞれ解説していきます。

波源 〜 反射板の区間（重要）

特徴

波源 〜 反射板の区間は、同じ波長・振幅をもつ入射波と反射波が逆向きに進んでいるので、定常波（定在波）が発生します。

補足
逆行する2つの正弦波を重ね合わせると、定常波（定在波）と呼ばれる、その場で振動する波ができます。
元の波の波長を λ\lambda 、振幅を AA と置くと、できる定常波の波長は λ\lambda 、振幅は 2A2A となります。
振幅が最大の点を腹、一切振動しない点を節といい、腹同士の間隔（腹間隔）は波長の半分の λ2\dfrac{\lambda}{2} になります。
Desmos のグラフはこちら
グラフのみを表示

補足にある通り、入射波が波長 λ\lambda 、振幅 AA の時、波長 λ\lambda 、振幅 2A2A の定常波が生じます！

重要な点は、反射板上の媒質が自由端反射の場合は腹に、固定端反射の場合は節になることです。（上の画像を参照してください！）

補足にあるように、腹は定常波において最も振幅が大きい点（つまり今回であれば振幅が 2A2A の点）でした。だからこそ自由に端が動くので自由端反射になるわけです。

同様に、節は定常波において全く振動しない点であるので、端が全く動かない固定端反射になります。

合成波の表式

合成波の表式を計算できることも重要です。

入射波が

y入(x, t)=Asin⁡2π(xλ−tT) [m]y_{\textrm{入}}(x,\,t)=A\sin 2\pi \left(\frac{x}{\lambda}-\frac{t}{T}\right)\ [\mathrm{m}]

とかける時を考えます。 A, λ, TA,\,\lambda ,\,T はそれぞれ振幅, 波長, 周期を表しています。

自由端反射の場合

まずは反射波の表式を求めます。

上の図のように、反射波は入射波と壁について線対称となります。

よって、反射波の位置 xx における変位 y反(x, t)y_{\textrm{反}}(x,\,t) は、入射波の位置 2l−x2l-x における変位 y入(2l−x, t)y_{\textrm{入}}(2l-x,\,t) に等しくなります！（ x, 2l−xx,\ 2l-x の中点が壁 ll になります ）

従って、反射波は

y反(x, t)=y入(2l−x, t)=Asin⁡2π(2l−xλ−tT) [m]\begin{align*}y_{\textrm{反}}(x,\,t)&=y_{\textrm{入}}(2l-x,\,t)\\ &=A\sin 2\pi \left(\frac{2l-x}{\lambda}-\frac{t}{T}\right)\ [\mathrm{m}]\end{align*}

と表せます！

求める合成波は入射波と反射波を足し合わせたものであるので、

y合(x, t)=y入(x, t)+y反(x, t)=Asin⁡2π(xλ−tT)+Asin⁡2π(2l−xλ−tT)=2Asin⁡2π(lλ−tT)cos⁡2π(x−lλ)[m]\begin{align*} y_{\textrm{合}}(x,\,t) &=y_{\textrm{入}}(x,\,t)+y_{\textrm{反}}(x,\,t)\\ &=A\sin 2\pi \left(\frac{x}{\lambda}-\frac{t}{T}\right)+A\sin 2\pi \left(\frac{2l-x}{\lambda}-\frac{t}{T}\right)\\ &=2A\sin 2\pi \left(\frac{l}{\lambda}-\frac{t}{T}\right)\cos 2\pi \left(\frac{x-l}{\lambda}\right) [\mathrm{m}] \end{align*}

と求まります！（最後は和積の公式を用いました）

固定端反射の場合

まずは反射波を求めますが、自由端反射と違う点は、反射波が上下方向にも線対称になっている点です。（左右方向と上下方向に折り返すと、点対称の位置関係になります）

よって、自由端反射の場合の反射波の符号を反転させれば良いので、

y反(x, t)=−y入(2l−x, t)=−Asin⁡2π(2l−xλ−tT) [m]\begin{align*}y_{\textrm{反}}(x,\,t)&=-y_{\textrm{入}}(2l-x,\,t)\\ &=-A\sin 2\pi \left(\frac{2l-x}{\lambda}-\frac{t}{T}\right)\ [\mathrm{m}]\end{align*}

と表せます！（マイナスがつきました）

求める合成波は入射波と反射波を足し合わせたものであるので、

y合(x, t)=y入(x, t)+y反(x, t)=Asin⁡2π(xλ−tT)−Asin⁡2π(2l−xλ−tT)=2Acos⁡2π(lλ−tT)sin⁡2π(x−lλ)[m]\begin{align*} y_{\textrm{合}}(x,\,t) &=y_{\textrm{入}}(x,\,t)+y_{\textrm{反}}(x,\,t)\\ &=A\sin 2\pi \left(\frac{x}{\lambda}-\frac{t}{T}\right)-A\sin 2\pi \left(\frac{2l-x}{\lambda}-\frac{t}{T}\right)\\ &=2A\cos 2\pi \left(\frac{l}{\lambda}-\frac{t}{T}\right)\sin 2\pi \left(\frac{x-l}{\lambda}\right) [\mathrm{m}] \end{align*}

と求まります！

波源より先の区間

波源より先は、同じ波長・振幅をもつ入射波と反射波が同じ方向に進むので、進行波が発生します。（つまり普通の正弦波が発生します）

波長は進行波と等しくなるので分かりやすいですが、注意すべきは振幅です。

進行波は定常波とは異なり、どの点も振幅が等しいです。よって、波源位置の振幅こそが進行波の振幅に等しくなります。

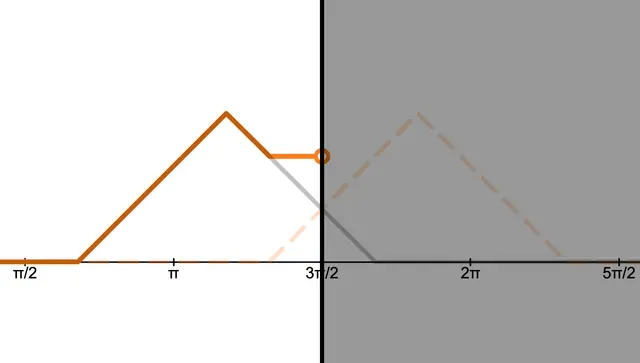
このとき、上のグラフを見るとわかるように、波源位置において定常波と進行波は連続して（＝つながって）います！よって、波源位置における定常波の振幅こそが、進行波の振幅に一致します。

つまり振幅は波源ー反射板の距離に依存するので、次の図のように波源が定常波の節となると波は発生しません。

SHARE
<
jiyukotesee
【グラフで遊ぶ】固定端・自由端反射を見よう
jiyukotebetween1
固定端・自由端反射の中間という謎（前編）
>
Images are created with the Desmos Graphing Calculator, used with permission from Desmos Studio PBC.
© 2024 UNS Physics. All Rights Reserved.