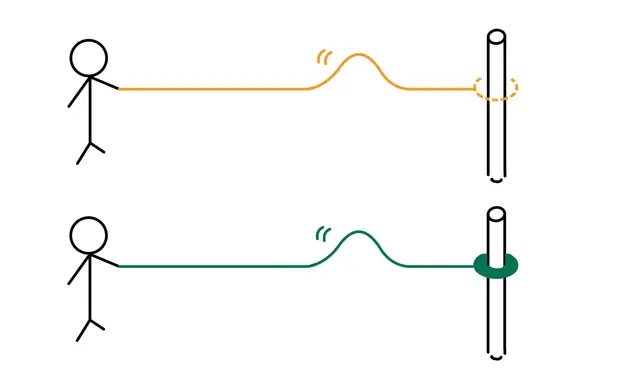
波は反射する際、波の種類などによって固定端反射なのか自由端反射なのかが変わります。

端が自由に動けば反射波の位相は変化せず、自由端反射となり、端が完全に固定されていれば反射波の位相は $\pi$ 変化して、固定端反射となります。

では端が絶妙に動きにくい時など、自由端と固定端の中間はどうなるのでしょうか？
もしくは光波の時に2つの屈折率が同じ場合はどうなるのでしょうか？

実は透過波が存在する時は反射波の位相は 0 と $\pi$ に限られ、透過波が存在しない全反射の時は位相変化は 0 と $\pi$ の中間の値を取り得ます。

文章では分かりにくいのでグラフで実際に確認してみましょう！

長くなるのでこの記事ではまず透過波がある場合を考えます。

透過波が存在する場合

透過波が存在する光波の場合、グラフは以下の通りです。

（以下、屈折率 $n_1$ の媒質から屈折率 $n_2$ の媒質に入射する時、 $\dfrac{n_2}{n_1}$ のことを屈折率比と呼ぶことにします。）

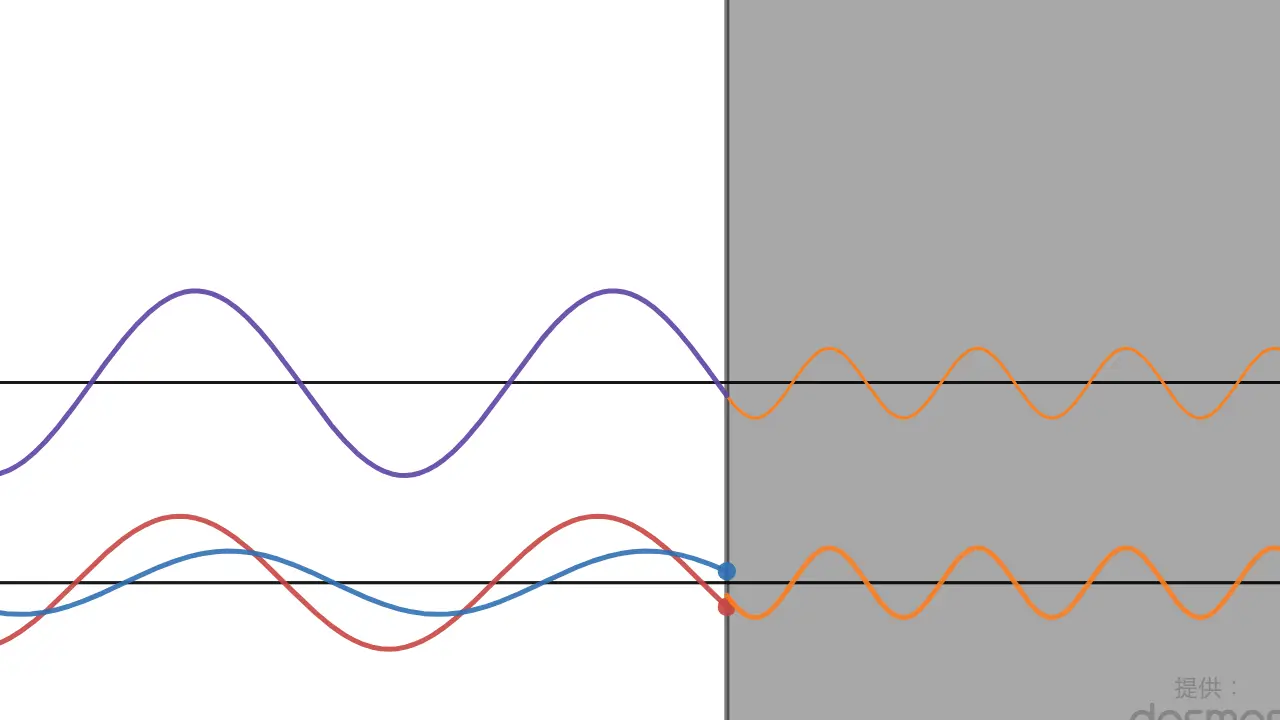
下側のグラフは入射波・反射波・透過波を表していて、上側のグラフはそれらの合成波、つまり実際に観測できる波を表しています。

まずは屈折率比が最大の時に反射波の位相が $\pi$ ずれて固定端反射に、屈折率比が最小の時に位相はズレずに自由端反射になることを確認してみてください。
この時は共に反射率が100%に近くなることも重要です。

ではその中間はどうなっているのか見てみましょう。
START / STOP ボタンを押してグラフをストップさせた状態で屈折率比を動かしてみてください。

屈折率比 ＜ 1のとき

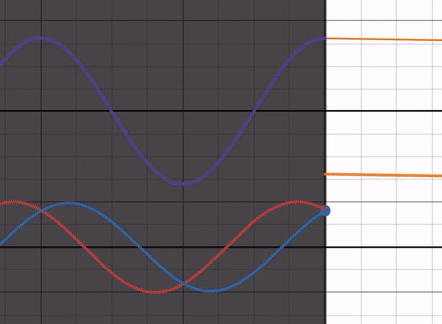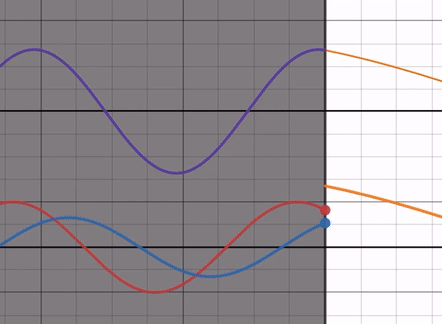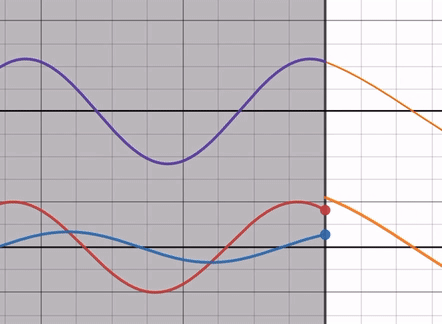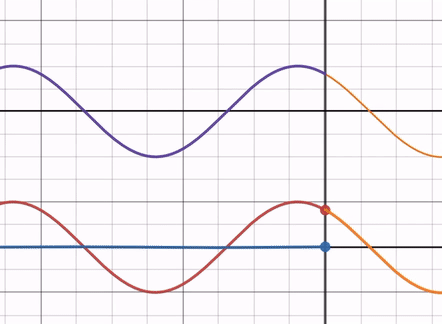
屈折率比を min → 1 まで動かしてみると、反射波の振幅が 0 に近づいていきます。反射波の位相は屈折率比に依存せず、常に入射波と位相差が 0 であることに注意してください（ $x$ 切片などに注目すると位相が変化していないことが分かる）。

この時、反射波の端は入射波の端と同じ側にあるので、自由端反射に近い状態であると言えます。

つまり自由端反射になる場合に比べると、ただ反射波の振幅が小さくなっているということです。

屈折率比 ＞ 1のとき

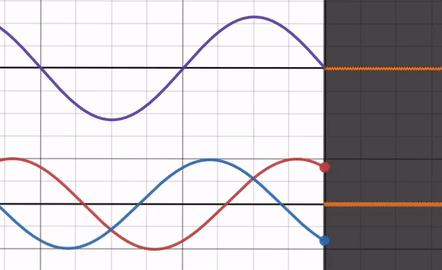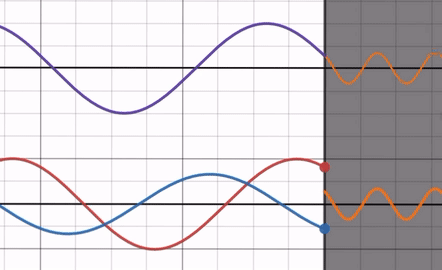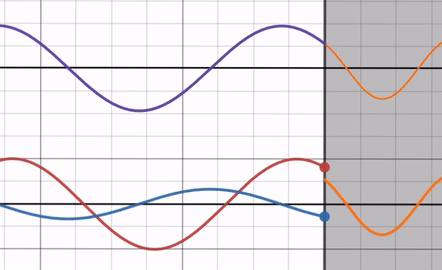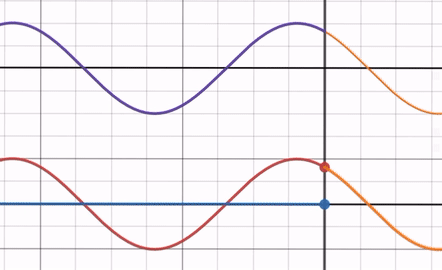
屈折率比を Max → 1 まで動かしてみると、反射波の振幅が 0 に近づいていきます。反射波の位相は屈折率比に依存せず、常に入射波と位相差が $\bm\pi$ であることに注意してください（ $x$ 切片などに注目すると位相が変化していないことが分かる）。

この時、反射波の端は入射波の端と逆側にあるので、固定端反射に近い状態であると言えます。

つまり自由端反射になる場合に比べると、ただ反射波の振幅が小さくなっているということです。

屈折率比 = 1 のとき

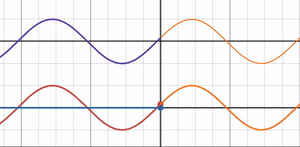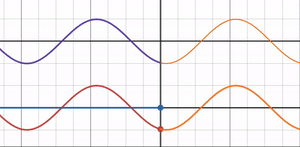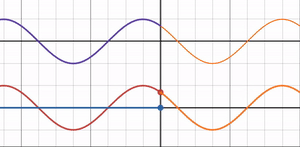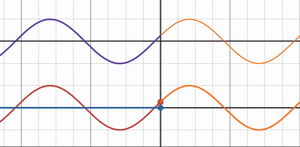
では自由端反射と固定端反射の丁度中間である屈折率 = 1の時はどうなるのでしょうか？

グラフを見ると反射波の振幅が 0 となり、反射率も 0 になることが分かります。

よく考えればわかることですが、屈折率比 = 1ということは光波が通過する媒質が変化しないということなので、光波は反射せず全て透過します。

考察

これで光波の位相が屈折率比によって急に $\pi$ 変化する様子が納得できたのではないでしょうか？

このように、反射波の位相が急に $\pi$ 変化するというよりは、反射波の振幅がだんだん減って逆向きになると言った方が現実に近いと思います。

むしろ現実は中間

では実際に光の干渉実験を行う際などの状況において屈折率比はどの程度なのでしょうか？

有名な光の干渉実験としてニュートンリングが挙げられます（細かい実験の説明は省きます）。この場合は空気とガラスとの間で反射が起こりますが、その際の屈折率比は約 1.46（逆向きなら約 0.68 ）です。

グラフで確認すると分かると思いますが、この場合は反射率が約 3.6 %と低いので反射板上の合成波の変位は 自由端 or 固定端 とは到底言えない動きをしています。現実は中間なのです。

しかし、重要なのは反射波の変位が「正確に $\bm{\pi}$ 変化する or 全く変化しない」のどちらかに必ずなることです。これにより、光の干渉の実験においては屈折率比と1の大小関係さえ気をつければいいことが分かります。

入射波と透過波の振幅はほとんど変わらないことを考慮すると、ニュートンリングにおいて干渉する二つの光の振幅はほとんど同じであることも分かります。（二つとも一度反射する時においてのみ振幅が大きく減るが、減る度合いはほとんど同じであるため）