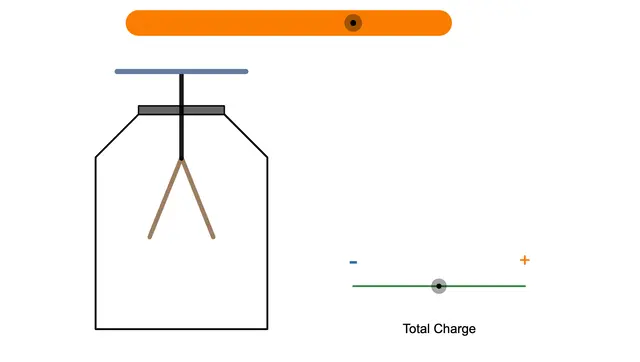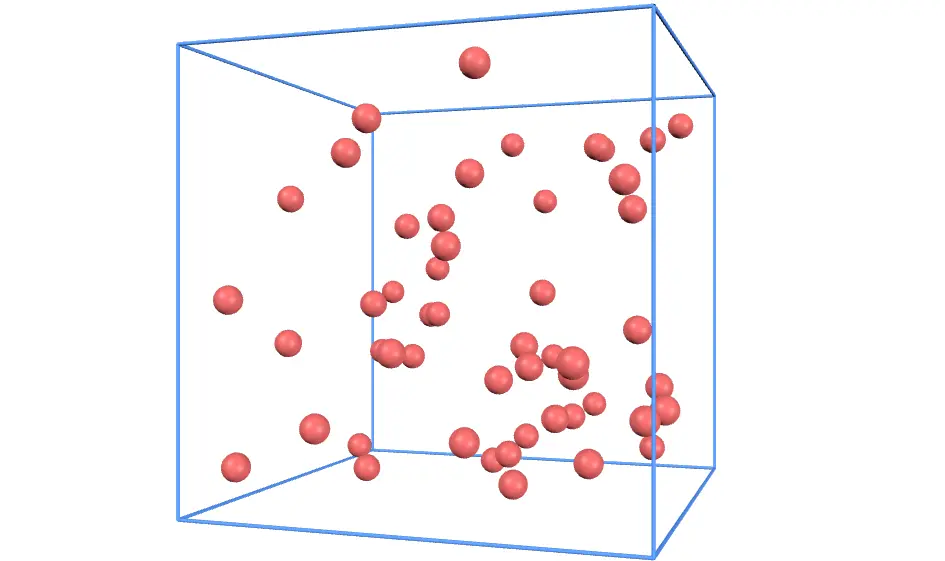
気体分子運動論を知っていますか？気体分子がどのように振る舞っているのかをグラフでシミュレーションしてみましょう！その後、気体分子と気圧の関係について学んでいきます。

アニメーション

容器内部をたくさんの気体分子が飛び交っている様子を表しています。追加 削除 ボタンを押すと気体分子を追加・削除することができます。

ただし、分子間力は無視しています。気体分子は壁とのみ弾性衝突をします。

ちなみに、グラフ右上の設定からグラフを白黒反転させることができますが、カッコいい見た目になるのでおすすめです！

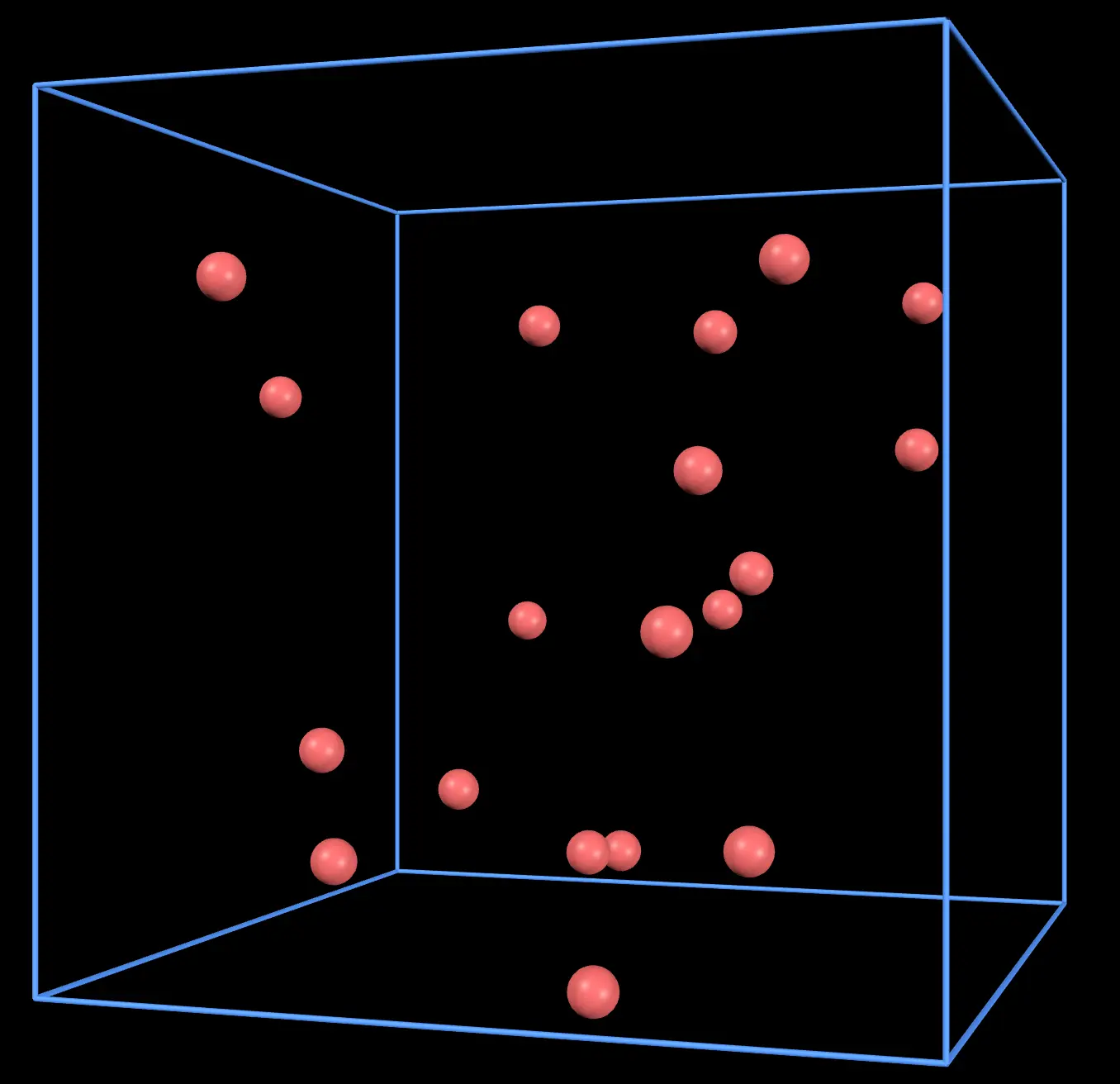
気体分子の振る舞い

空気中には目には見えない小さな気体分子が無数に飛び回っています。

地球上の物体は重力を受けるので、基本的にすべての物体は下へと落ちていくはずですが、気体分子のようにとても軽い粒子にとっては重力の影響は小さいです。よって、重力にある程度逆らって縦横無尽に飛び回る事ができるのです。

気圧

気圧とは

では、普段耳にする気圧とは何でしょうか？

気圧は、その名の通り「気体の圧力」です。圧力は力を面積で割ったものになります。つまり気圧は、単位面積あたりの壁がどれだけ気体分子から力を受けているかを表します。これだけだとわかりにくいので、先程のアニメーションで考えてみます。

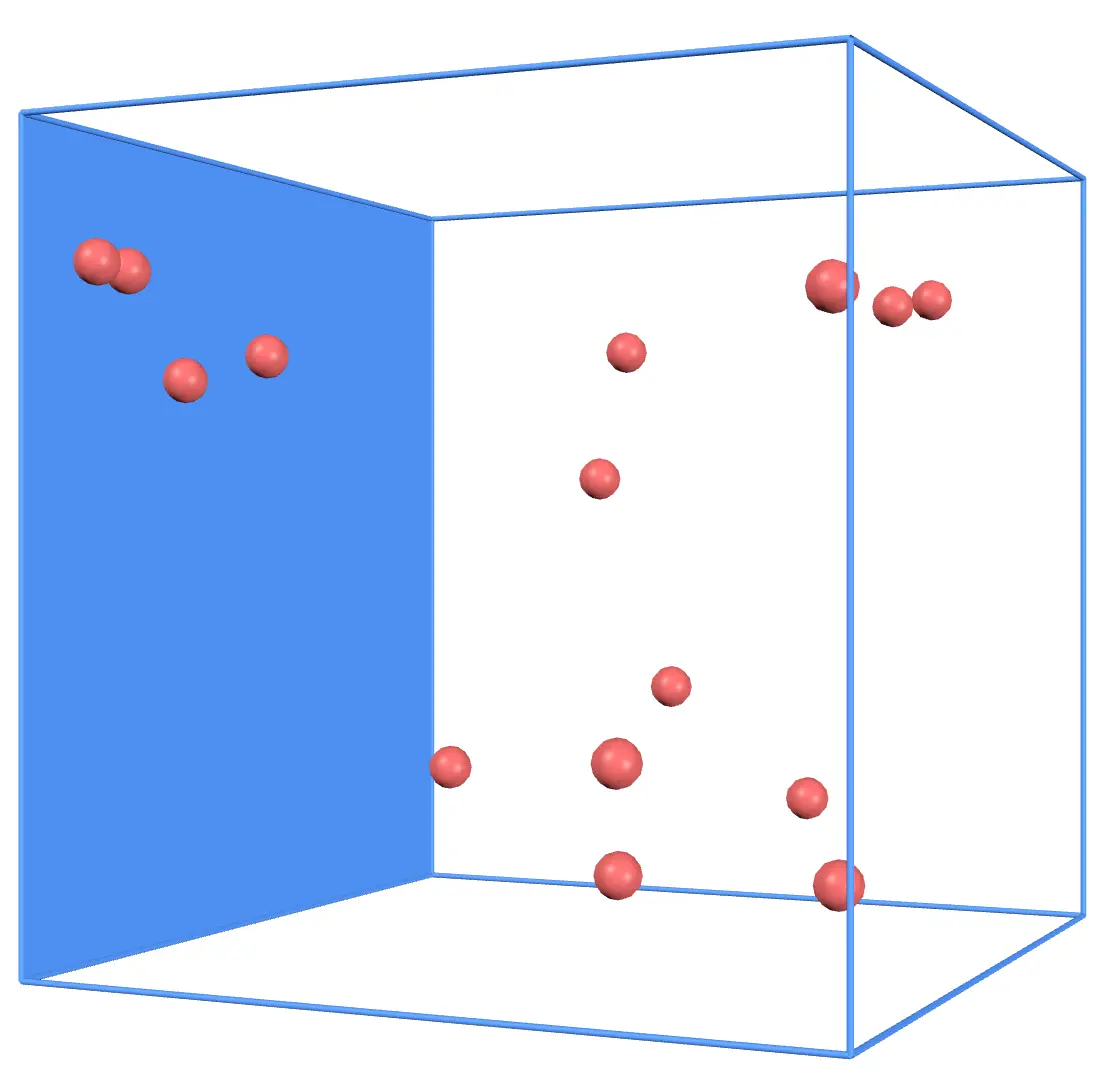
上の図のように１つの壁を考えてみます。

この壁に対してたくさんの気体分子が弾性衝突をするわけですが、このとき気体分子は壁に対して力を与えています。具体的には、気体分子１つにつき、平均して

の力を与えます。（導出は省略します）ただし、$m$ は気体分子１つの質量、$\overline{v^2}$ は気体分子の速さの２乗の平均値、$l$ は容器の１辺の長さを表しています。

気体分子が $N\ [\textrm{個}]$ 存在するとき、全分子が与える力は

です。気圧は、この力を壁の面積 $l^2$ で割ったものになります。つまり、

が求める気圧になります。ただし容器の体積を $V\,(=l^3)$ としました。単位は $\mathrm{Pa}$パスカル$=\mathrm{N/m^2}$ になります。

気圧の性質

では、先程の式をアニメーションと合わせて見ていきましょう！先程の式

の性質として、以下の点が挙げられます。

まずは体積を変化させてみましょう。スライダーを動かして辺の長さを小さくすると、このようになります。

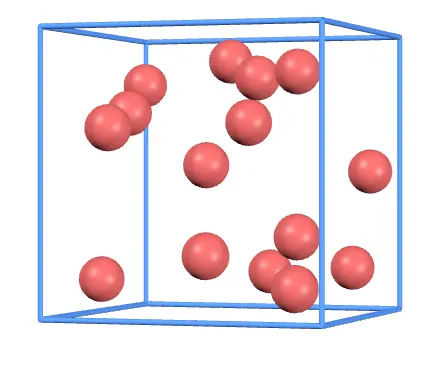
容器が小さい分、気体分子が壁に衝突する回数が増えます。よって壁に与える力も増えるので、気圧は大きくなります。

次に分子数を増やしてみましょう。容器の大きさを戻してから、追加 ボタンを何度か押してみましょう。このように分子数が増えたはずです。

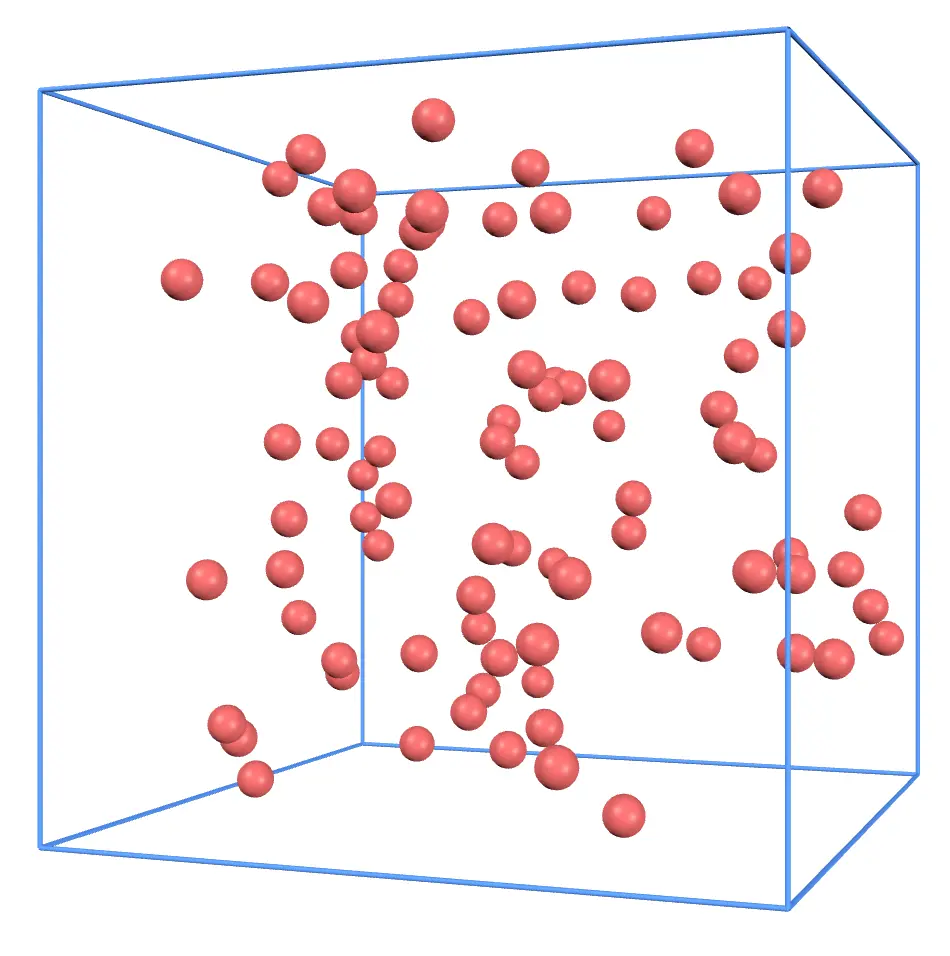
分子数が増えた分、気体分子が壁に衝突する回数が増えます。よって壁に与える力も増えるので、気圧は大きくなります。

同様に気体分子の速度も増やしてみてください。粒子の速度が上がると、その分壁に与える力も増えます。よって気圧は大きくなります。

温度との関係

では温度とはどのように関係するのでしょうか？

（理想）気体について、以下の状態方程式が成立します。

ただし、 $n$ は気体のモル数、$T$ は気体の温度です。ここに先程の $p$ を代入すると、

ここで、アボガドロ数 $N_A$ を用いて $N=nN_A$ が成立するので、整理すると

となり、ボルツマン数 $k=\dfrac{R}{N_A}$ という定数を用いると

という式が成立します。

左辺は明らかに気体分子の運動エネルギーを表しています。右辺は温度 $T$ を定数倍したものです。つまり、気体分子の運動エネルギーと気体の温度は比例します！

このように、気体を大きな（マクロな）視点で見たときの物理量 $p,\,T$ と小さな（ミクロな）視点で見たときの物理量 $m,\,v$ を簡単な等式で結ぶことができるという点が、気体分子運動論で導かれる美しい帰結になります。