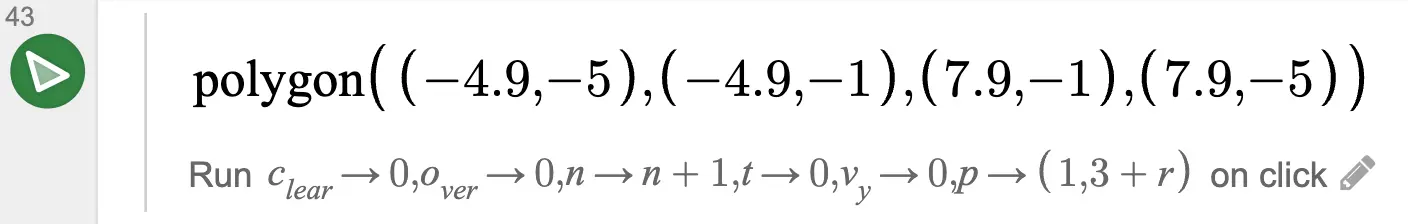UNS物理
Desmosでゲームを作ってみました
作成日：2025/3/18

Desmos を用いて簡単な障害物回避ゲームを作ってみました！どのようにすればゲームを作れるか、作り方を共有しようと思います。

完成したゲーム

Desmos のグラフはこちら
グラフのみを表示

START/STOP ボタンを押すと動き出します。紫色の障害物をすべて避けることができればゲームクリアです！

基本的な仕組み

詳しくはリンク先のグラフを見てもらうのが早いですが、ここでは基本的な仕組みについて解説します。

ティッカーでグラフを更新する

Desmos では、ティッカーを用いることで一定時間ごとに変数の値を更新することができます。詳しくはこちらの記事をご覧ください。

Desmosの使い方 アクション（操作）・ティッカー

ゲームを作る際は、このティッカーを用いてグラフを更新していくことが基本となります。具体的には、一定時間ごとにプレイヤーの座標を更新や当たり判定等の確認を行います。

プレイヤー

プレイヤーの座標と鉛直方向の速度をそれぞれ p,vyp,v_y という変数で管理しています。rr は大きさ（半径）です。

1
p=(1,3.5)p=(1,3.5)
2
vy=0v_y=0
3
r=0.5r=0.5
4
(x−p.x)2+(y−p.y)2≤r2(x-p.x)^2+(y-p.y)^2\leq r^2

プレイヤーを円で描画することで、後の当たり判定が楽になるようにしています。

p.xp.x のようにすることで、pp の xx 座標を参照することができます。

障害物

障害物はリストで作り、同様に円で描画しています。

1
障害物の平均間隔\textrm{障害物の平均間隔}
2
dball=16d_{ball}=16
3
障害物の個数\textrm{障害物の個数}
4
nball=20n_{ball}=20
5
障害物の速さ\textrm{障害物の速さ}
6
vball=0.02v_{ball}=0.02
7
障害物の初期 x 座標\textrm{障害物の初期 }x\textrm{ 座標}
8
Ox=dball⋅[1,...,nball]O_{x}=d_{ball}\cdot[1,...,n_{ball}]
9
障害物の半径\textrm{障害物の半径}
10
R=0.3R=0.3
11
(x−(Ox−vballt))2+(y−(R+3))2≤R2(x-(O_{x}-v_{ball}t))^{2}+(y-(R+3))^{2}\le R^{2}

これで、 2020 個の障害物が速さ 0.020.02 で左に移動します。これだけでもいいのですが、実際には障害物の位置や半径を乱数を用いてバラしています。

1
障害物の初期 x 座標\textrm{障害物の初期 }x\textrm{ 座標}
2
Ox=[5i for i=random(nball,n)]+dball⋅[1,...,nball]O_{x}=[5i\ \mathrm{for}\ i=\mathrm{random}(n_{ball},n)]+d_{ball}\cdot[1,...,n_{ball}]
3
障害物の半径\textrm{障害物の半径}
4
R=[2i for i=random(nball,n)]+0.3R=[2i\ \mathrm{for}\ i=\mathrm{random}(n_{ball},n)]+0.3

random(a,b) とすると、aa 個の乱数のリストを生成できます。bb は乱数生成のシード値です。つまり bb を変えることで異なる乱数を生成できます。後に用います。

座標の更新

ティッカーで実行するアクションは以下のようです。

1
T(d)=t→t+dT(d)=t\to t+d
2
Py(d)={p.y+dvy≥3+r:p→(p.x,p.y+dvy), p→(p.x,3+r)}P_y(d)=\{p.y+dv_{y}\ge 3+r:p\to (p.x,p.y+dv_{y}),\ p\to (p.x,3+r)\}
3
Vy(d)={p.y>3+r:vy→vy−dg,vy→0}V_{y}(d)=\{p.y>3+r:v_{y}\to v_{y}-dg,v_{y}\to0\}

引数 dd にはティッカーで用いることができる特殊な変数である dt\mathrm{dt} を指定します。これによって、dd にはティッカーの前回実行してからの経過時間が代入されます。こちらについても、先程載せたこの記事で詳しく説明しています。

Desmosの使い方 アクション（操作）・ティッカー

これらのアクションについてそれぞれ説明します。

まず、TT は経過時間を足すことで時刻 tt を更新しています。

PyP_y はプレイヤーの yy 座標を更新しています。基本的には 速度 ✕ 経過時間 を座標に足していますが、地面を下に突き抜けそうなときは地面に接するように更新します。3+r3+r は地面の yy 座標とプレイヤーの半径の和になっています。つまり、地面に接したときのプレイヤーの yy 座標です。

VyV_y はプレイヤーの鉛直方向の速度を更新しています。基本的には 重力加速度 ✕ 経過時間を引いていますが、こちらも地面に接しているときは例外で、速度を 00 にするようにしています。

ボタンで操作

ボタンを押すことでプレイヤーはジャンプします。これはグラフをクリック時にアクションを実行することで実現しています。

1
ジャンプ時の初速度\textrm{ジャンプ時の初速度}
2
jump=0.07j_{ump}=0.07
3
Jump=p→(p.x,p.y+0.01),vy→jumpJ_{ump}=p\to(p.x,p.y+0.01),v_{y}\to j_{ump}

上のように定義されたアクションを

のように、polygon で作られたボタンをクリックしたときに実行しています。

速度を変化させているだけでなく、わざわざプレイヤーを少し上にずらしているのは、地面から離れた判定にするためです。

当たり判定・クリア判定

障害物と衝突したかどうかの判定も重要です。これは、障害物との距離を考えることで判定しています。

1
Collision={min((Ox−vballt−p.x)2+(R−(p.y−3))2(R+r)2)≤1:over→1}C_{ollision}=\left\{ \mathrm{min}\left(\dfrac{(O_{x}-v_{ball}t-p.x)^{2}+(R-(p.y-3))^{2}}{(R+r)^{2}}\right)\le1:o_{ver}\to1\right\}

見た目は複雑ですが、していることは簡単です。分子 (Ox−vballt−p.x)2+(R−(p.y−3))2(O_{x}-v_{ball}t-p.x)^{2}+(R-(p.y-3))^{2} は障害物とプレイヤーの中心間距離の２乗です。分母 (R+r)2(R+r)^{2} は半径の合計を２乗したものです。つまり、この分数が 11 より小さければ、障害物とプレイヤーの中心間距離が半径の合計より小さいことになるので、衝突しています。

厳密には障害物は複数あるので、この分数はリストになっています。この分数の最小値が 11 より小さければ、少なくとも１つの障害物に衝突していることになります。

この衝突判定をティッカーで実行することで、毎回の更新時に衝突しているかを判定しているわけです。

クリア判定も同様です。

1
Clear={max(Ox[Ox.count]−vballt+3,over)≤0:clear→1}C_{lear}=\left\{\mathrm{max}(O_{x}[O_{x}.\mathrm{count}]-v_{ball}t+3,o_{ver})\le0:c_{lear}\to1\right\}

Ox[Ox.count]O_{x}[O_{x}.\mathrm{count}] は OxO_x の最後の要素、つまり最後の障害物の初期 xx 座標です。つまり、Ox[Ox.count]−vballt+3O_{x}[O_{x}.\mathrm{count}]-v_{ball}t+3 は最後の障害物の少し右側の xx 座標です。これが 00 以下になったらクリアになるようにしています。もちろん、ゲームオーバー状態でないことも確認しています。

リトライボタン

リトライボタンを押すことで、様々な変数を元に戻しています。

注目すべきは n→n+1n\to n+1 としていることです。nn は障害物を生成する乱数のシード値でした。これをリトライ時に変えることで、障害物の大きさや位置を別のものに変えています。

Tips

レスポンシブなグラフ

Desmos のグラフを作成するときの大きな悩みポイントとして、画面サイズの違う端末で見たり、グラフを拡大縮小したりすると、グラフが崩れてしまうことがある点が挙げられます。

例えば、画面の大きなタブレットでこのようなグラフを作成します。

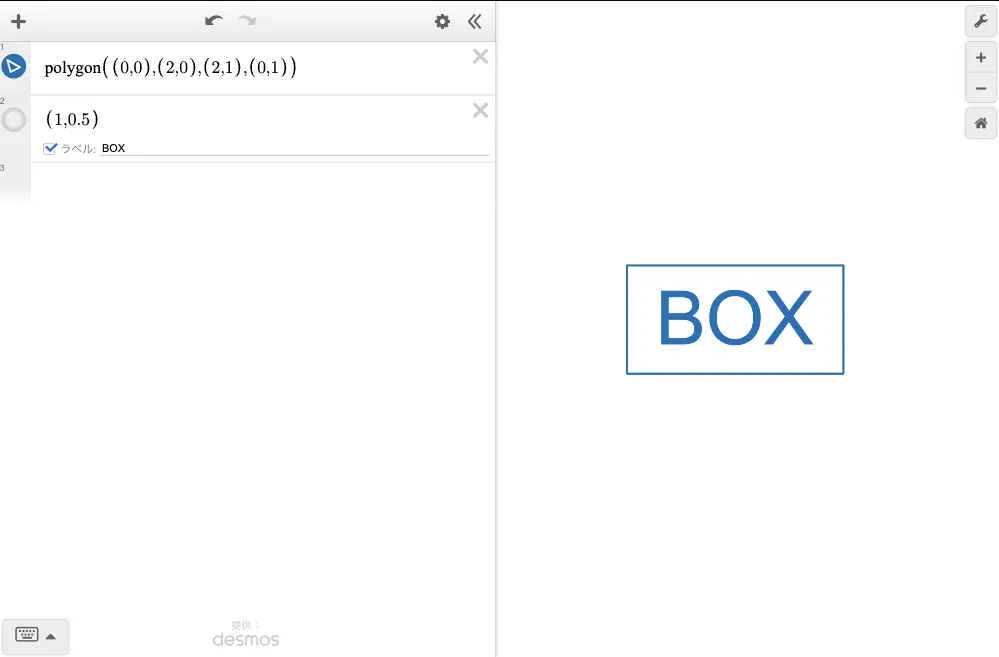
このとき、このグラフをスマートフォンで開くとこのようになります。

BOX というラベルが大きめに表示され、レイアウトが崩れてしまっています。

これは、ラベルの大きさが画面サイズに応じて見やすくなるように変更されてしまっているからです。

このようなレイアウト崩壊を防ぎ、レスポンシブなグラフを作るためには２つのポイントがあります。それは以下のようです。

レスポンシブなグラフのポイント

  • ラベル（点）の大きさは width\mathrm{width} を用いて指定する
  • グラフの表示域を固定する

Desmos には、画面サイズを表す特殊な変数である width\mathrm{width} があります。これを用いてラベルの大きさを指定することで、画面サイズが変わってもラベルの相対サイズは不変になります。

具体的には、

1
s=0.002widths=0.002\mathrm{width}

のようにして、この ss を用いてラベルの大きさを指定します。

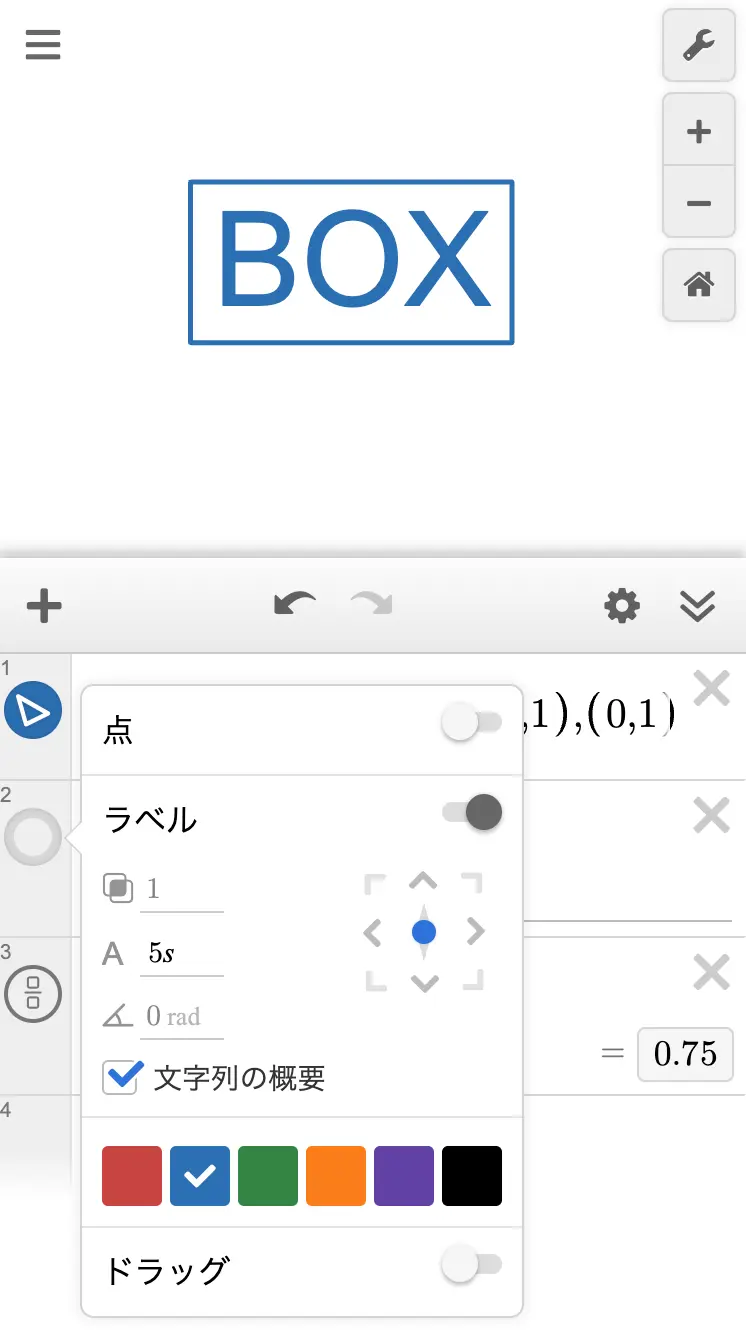
すると、BOX がきれいに収まってくれました。

このとき、表示域を固定することもポイントです。ラベルの大きさはグラフを拡大縮小しても変わらないので、拡大縮小によるレイアウト崩壊を防ぐためには、表示域を固定することが有効です。

グラフを軽くする

今回のゲームでは、障害物がたくさん存在するので、このままだとグラフが重くなってしまいます。そこで描画や当たり判定を行う対象を、画面内に存在する障害物のみにしています。

具体的には、

1
m=floor(vballtdball)m=\mathrm{floor}\left(\dfrac{v_{ball}t}{d_{ball}}\right)
2
(x−(Ox[m,...,m+2]−vballt))2+(y−(R[m,...,m+2]+3))2≤R[m,...,m+2]2(x-(O_{x}[m,...,m+2]-v_{ball}t))^{2}+(y-(R[m,...,m+2]+3))^{2}\le R[m,...,m+2]^{2}

のようにすることで、画面内に存在する可能性のある障害物のみを描画することができます。

SHARE
<
Desmosでギリシャ文字を入力したい
DesmosAPI GraphingCalculator.controller.dispatch() の使い方
>
Images are created with the Desmos Graphing Calculator, used with permission from Desmos Studio PBC.
© 2024 UNS Physics. All Rights Reserved.