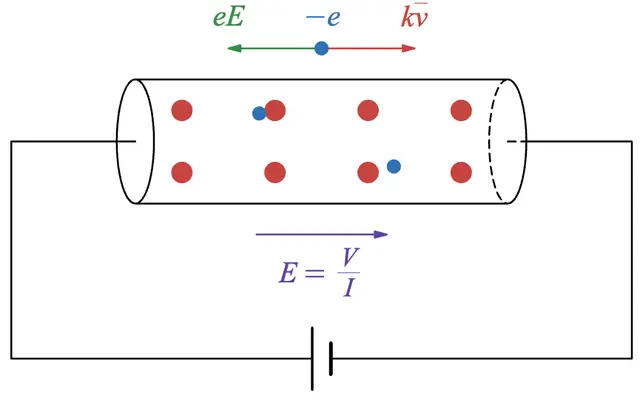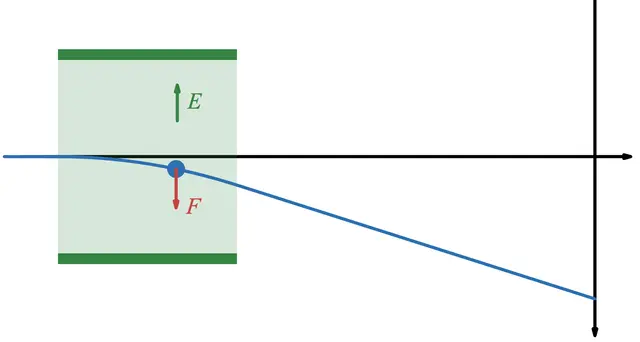
今回は、導体中の電子の振る舞いをシミュレーションを通して見てみましょう！その後、静電遮蔽と呼ばれる現象について紹介します！

電子のシミュレーション

START/STOP ボタンを押すと、電子が動き出します。互いに反発する様子が観察できるでしょうか？

電場の表示というスイッチを入れると緑色で電場が表示されますが、動作が重くなります。

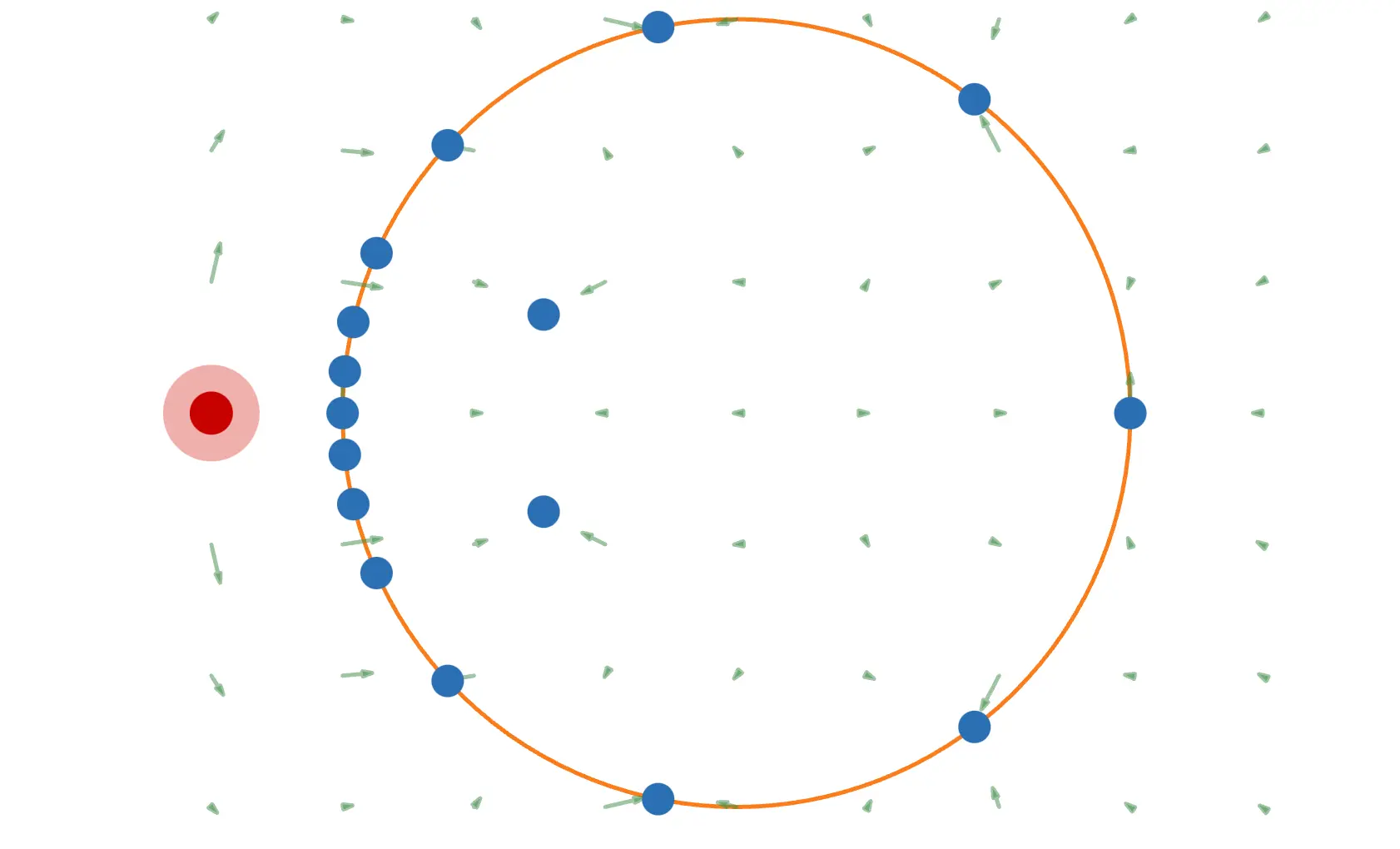
外部の電荷というスライダーを動かすと、外部に電荷を出現させられます。内部の電子や電場にどのような影響を与えるでしょうか？外部の電荷はドラッグで動かせます。

導体の特徴

導体とは、電気を通しやすい物質を指します。代表例が金属です。

金属内部には、自由電子と呼ばれる自由に金属内を動くことができる電子が無数に存在しています。この自由電子が電気を運んでくれます。

導体は以下のような特徴を持ちます。

内部に電場は無し

まず1つ目の特徴として、導体内部には電場は存在しません。

理由はとても簡単で、もし電場が存在するならば、電場から力を受けた自由電子が電場を打ち消す向きに運動を始めてしまうからです。

導体内には自由電子が無数にあるので、電場がなくなるまで自由電子は移動し続けます。よって、自由電子が動き切った時には内部の電場は無くなっているはずです。

内部の電位は一定

2つ目の特徴として、導体内部の電位は一定となります。

これも理由は簡単です。内部の電場が存在しないことと、内部の電位が一定であることは同値であるからです。

電位とは、$1\,\mathrm{C}$ あたりの電荷が持つ位置エネルギーを指します。内部に電場が存在しない時、電子が受ける力は存在しないので、内部の電子が持つ位置エネルギーは全て等しくなります。つまり、電位は全て等しくなるわけです。

シミュレーションで確認

では、これらの特徴をシミュレーションで確認してみましょう。

START/STOP ボタンを押してしばらく経った後、電場を表示するスイッチを入れてみてください。

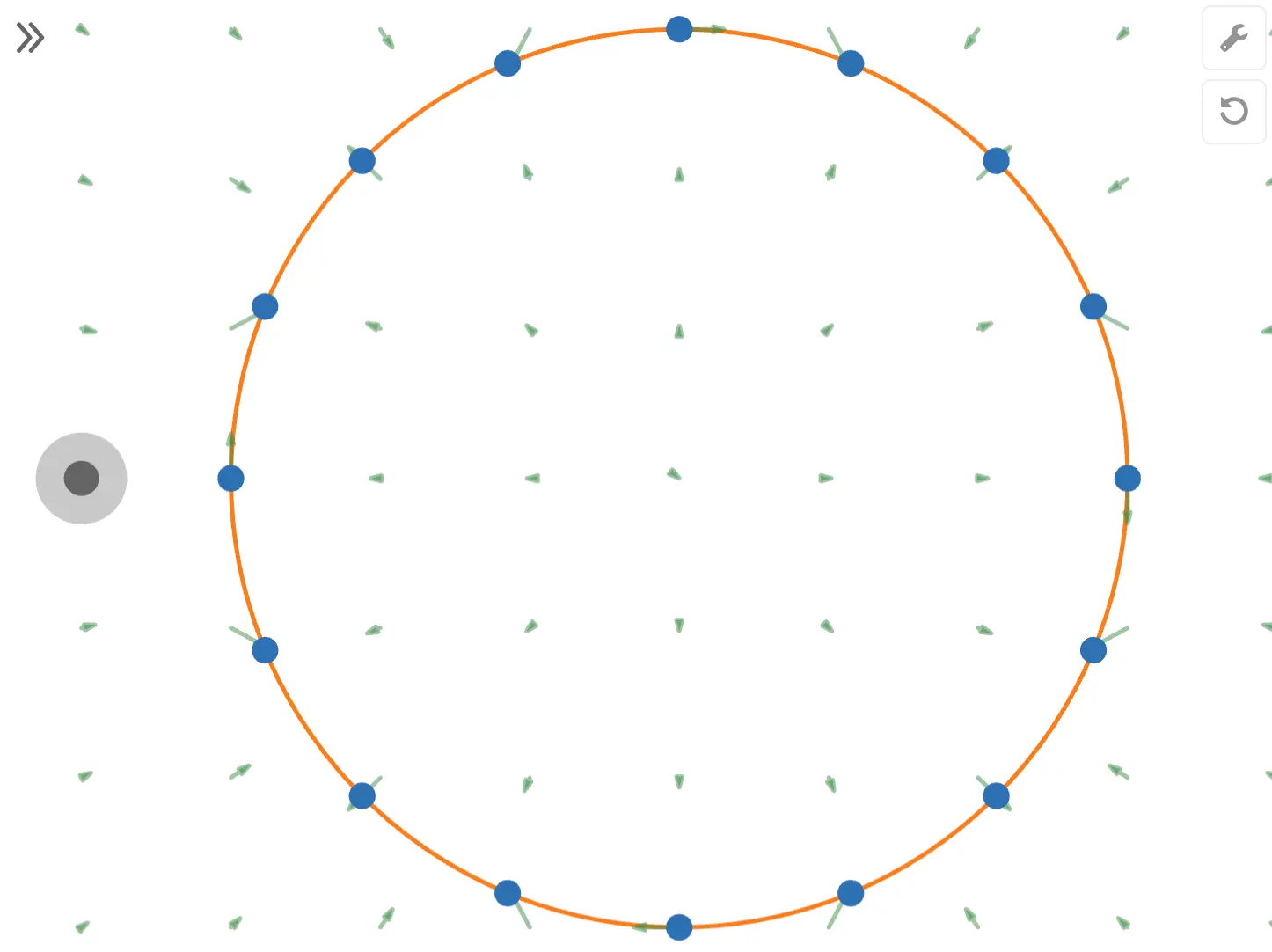
上の画像のようになったでしょうか？導体内部に電場が存在しないことが確認できると思います。

外部に電荷があるときも同様です。是非試してみてください！

静電遮蔽

これらの性質により、導体の容器を用意すると、外部の電場を遮断することができます。これを静電遮蔽と言います。

図のように、外部の電気力線を導体中の電子が吸収してくれます。よって中まで電気力線が入り込まないので、導体容器の内部には電場が生じません。

厳密な議論（発展）

大学以降の知識を用いると、静電遮蔽を厳密に示すことができます。

位置 $\bm{r}=(x,y,z)$ におけるポテンシャル（電位）を $\phi(\bm{r})$ 、電荷密度（単位体積あたりの電荷）を $\rho(\bm r)$ 、誘電率を $\varepsilon$ とすると、以下のポアソン方程式が成立します。

ただし、$\Delta$ はベクトルの世界での微分を表します。書き下すと、

となります。$\partial$ は偏微分という特別な微分を表しますが、とりあえずは普通の微分だと考えてください。

このポアソン方程式は、大まかに言えば電位を２回微分したものが、電荷密度にマイナスをつけたものに等しいことを表しています。

今回、導体の容器の中身を考えます。中には電荷は存在していないので、電荷密度は $0$ です。式で書くと、

となります。

導体の電位は一定なのでこれを $c$ とおくと、導体と中身の境界上の電位（つまり導体の内側の表面の電位）は

を満たします。（これを境界条件と言います）

$(1),(2)$ と共に満たす電位として、どの点でも一定である

が考えられそうです。

実は境界条件が分かっている時、ポアソン方程式の解は一意に定まることが数学的に示せます！よって、これが求める電位になります。

電位が一定であるということは、中には電場が存在しないということです！