UNS物理
電磁波はどんな形？どうして発生？グラフをいじってみよう
electromagneticwave
作成日：2025/3/10

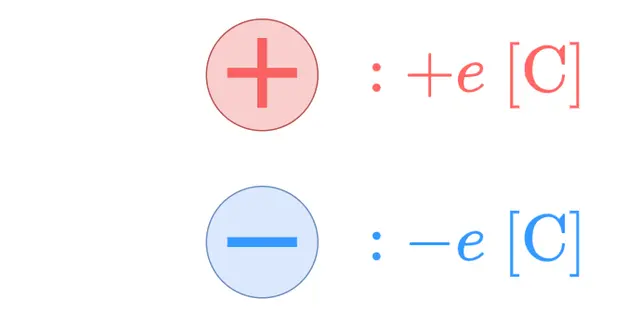
皆さんは電磁波とは何か知っていますか？今回は電磁波を実際にアニメーションを通して見てみましょう！

電磁波のアニメーション

電場

磁場

Desmos のグラフはこちら
グラフのみを表示

黄色で表示されている軸上に電磁波が存在しています。軸上の点の電場や磁場をベクトルで表示したものが、このアニメーションになります。

電場と磁場が横波として、互いに直交する平面上で進んでいることを確認しましょう！

電磁波の特徴

電磁波の大きな特徴として、

電磁波の特徴

  • 電場と磁場を媒質とした横波である
  • 電場と磁場は直交し、必ず共に存在する
  • 速さは一定で、光速に一致する
  • 波長によって性質が大きく変わる

があげられます。１つずつ見ていきましょう！

電場と磁場を媒質とした横波

波には、必ずその波を伝える媒質が必要です。例えば、水面波は水、音は空気が媒質となります。

そして、電磁波を伝える媒質は電場と磁場になります！電場と磁場については以下の記事をご覧ください。

elecore1
電磁気を根本から理解しよう① 〜電荷と電磁場とは〜

また、電場と磁場が波の進行方向に対して横向きに振動しているので、電磁波は横波です。

電場と磁場は直交して共に存在

次の特徴として、電場と磁場が互いに直交していることがあげられます。

電場が存在する面と磁場が存在する面が直交していることを、アニメーションを見て確認してみてください！

また、電場と磁場は必ず共に存在します。電場だけの波や磁場だけの波は存在しません！

電場と磁場が互いに直交して共に伝わっていく横波が電磁波になります。

速さは光速で一定

次に、電磁波の速さは一定であり、光の速度に一致します。

電磁波（光）の速さ ⋯ c=299 792 458 [m/s]（およそ秒速30万km）\begin{align*}\textrm{電磁波（光）の速さ}\ \cdots\ &c=299\,792\,458\,[\mathrm{m/s}]\\ &\textrm{（およそ秒速30万}\mathrm{km}\textrm{）}\end{align*}

これはとても重要で不思議な特徴です。普通は、物体の速さは観測者の速度に依存しますが、電磁波は誰からみても必ず一定の速さになるのです。

また、後述するように、僕たちがみている光は電磁波の１つになります。よって、光の速さと電磁波の速さは一致します。

波長により性質が変化

電磁波の性質は、その波長によって大きく異なります。

波長が 380 nm380\,\mathrm{nm} から 780 nm780\,\mathrm{nm} 程度の時、私たちは電磁波を目で感じ取ることができます。これを光（可視光線）と言います。

可視光線の中では、赤色が最も波長が長く、紫色が最も波長が短いです。赤色よりも波長が長い電磁波を赤外線、紫色よりも波長が短い電磁波を紫外線と言います。

赤外線よりも波長が長い電磁波を電波と言います。電波の中には、電子レンジで食べ物を温めるのに使われるマイクロ波や、携帯電話などで使われる電波も含まれます。意外と波長が大きいことを実感してもらいたいです。

紫外線よりも波長が短い電磁波には、X\mathrm X 線や γ\gamma 線が含まれます。とても波長が短いので、様々な物体を通り抜けることができ、X\mathrm X 線検査などに用いられています。

電磁波はなぜできる？（発展）

では、なぜ電磁場が発生するのかをみていきます。

簡単な説明

電場と磁場はそれぞれ電荷と電流によって発生しますが、それ以外にも時間変化をすると互いを誘起するという性質があります。

つまり、ある点における電場が時間変化をすると、周りに磁場を作り出します。逆に、磁場が時間変化すると、周りに電場を作り出します。

この２つの法則が無限ループしそうな気がしませんか？

例えば、ある点の電場が時間変化すると、

電場が時間変化 → 磁場が発生 ＝ 磁場が時間変化 → 電場が発生 ＝ 電場が時間変化 …

のような無限ループになります。これが電磁波の正体です！

マクスウェル方程式から導出

電場と磁場はマクスウェル方程式という４つの式を満たすように形成されます。

{∇⋅E=0∇⋅B=0∇×E=−∂B∂t∇×B=ε0μ0∂E∂t \left\{\hspace{6px}\begin{align*} &\nabla \cdot \boldsymbol{E} =0 \\[2px] &\nabla \cdot \boldsymbol{B} =0 \\[2px] &\nabla \times \boldsymbol{E} =-\frac{\partial \boldsymbol{B}}{\partial t} \\[7px] &\nabla \times \boldsymbol{B} =\varepsilon_0\mu_0\frac{\partial \boldsymbol{E}}{\partial t} \end{align*}\right.

ただし、E\bm E は電場、B\bm B は磁場、 ε0\varepsilon_0 は真空の誘電率、μ0\mu_0 は真空の透磁率を表しています。太字の文字はベクトルを表しています。

このマクスウェル方程式を用いると電磁波を導くことができますが、このままだと難しい演算子が含まれているので、（少し厳密性を欠きながらも）分かりやすく書き直すとこのようになります。

{dExdx+dEydy+dEzdz=0dBxdx+dBydy+dBzdz=0dEzdy−dEydz=−dBxdtdExdz−dEzdx=−dBydtdEydx−dExdy=−dBzdtdBzdy−dBydz=ε0μ0dExdtdBxdz−dBzdx=ε0μ0dEydtdBydx−dBxdy=ε0μ0dEzdt \left\{\hspace{6px}\begin{align*} &\frac{dE_x}{dx}+\frac{dE_y}{dy}+\frac{dE_z}{dz}=0 \\[7px] &\frac{dB_x}{dx}+\frac{dB_y}{dy}+\frac{dB_z}{dz}=0 \\[7px] &\frac{dE_z}{dy}-\frac{dE_y}{dz}=-\frac{dB_x}{dt} \\[7px] &\frac{dE_x}{dz}-\frac{dE_z}{dx}=-\frac{dB_y}{dt} \\[7px] &\frac{dE_y}{dx}-\frac{dE_x}{dy}=-\frac{dB_z}{dt} \\[7px] &\frac{dB_z}{dy}-\frac{dB_y}{dz}=\varepsilon_0\mu_0\frac{dE_x}{dt} \\[7px] &\frac{dB_x}{dz}-\frac{dB_z}{dx}=\varepsilon_0\mu_0\frac{dE_y}{dt} \\[7px] &\frac{dB_y}{dx}-\frac{dB_x}{dy}=\varepsilon_0\mu_0\frac{dE_z}{dt} \\[7px] \end{align*}\right.

もうぐちゃぐちゃです...

このままだと解くのが難しいので、電場と磁場が直交していることを用いて、電場は xx 成分のみ、磁場は yy 成分のみ存在することにします。つまり、それ以外の成分を 00 にすると、このようになります。

{dExdx=0dBydy=0dExdz=−dBydt−dBydz=ε0μ0dExdt \left\{\hspace{6px}\begin{align*} &\frac{dE_x}{dx}=0 \\[7px] &\frac{dB_y}{dy}=0 \\[7px] &\frac{dE_x}{dz}=-\frac{dB_y}{dt} \\[7px] &{-\frac{dB_y}{dz}}=\varepsilon_0\mu_0\frac{dE_x}{dt} \\[7px] \end{align*}\right.

これなら解けそうです！３つ目の式の両辺を zz で微分すると、

d2Exdz2=−d2Bydzdt=−d2Bydtdz=ddt(−dBydz)\frac{d^2E_x}{dz^2}=-\frac{d^2B_y}{dz dt}=-\frac{d^2B_y}{dt dz}=\frac{d}{dt}\left(-\frac{dB_y}{dz}\right)

ここに4つ目の式を代入して、

d2Exdz2=ddt(ε0μ0dExdt)=ε0μ0d2Exdt2\frac{d^2E_x}{dz^2}=\frac{d}{dt}\left(\varepsilon_0\mu_0\frac{dE_x}{dt}\right)=\varepsilon_0\mu_0\frac{d^2E_x}{dt^2}

実はこの式は、波動方程式という名前がついていて、波を表す式が解になります！

実際に、zz 軸方向に速さ 1ε0μ0\dfrac{1}{\sqrt{\varepsilon_0\mu_0}} で進む波は

Ex=Asin⁡(2πf(ε0μ0 z−t))E_x=A\sin \left(2\pi f\left(\sqrt{\varepsilon_0\mu_0}\,z-t\right)\right)

などと表すことができますが、これは先ほどの方程式を満たします！

よって、電場が速さ 1ε0μ0\dfrac{1}{\sqrt{\varepsilon_0\mu_0}} の波になることがわかります。実はこの速さを計算してみると、

1ε0μ0=299 792 458 m/s=c（光速）\frac{1}{\sqrt{\varepsilon_0\mu_0}}=299\,792\,458\,\mathrm{m/s}=c\textrm{（光速）}

となり、光速に一致します。つまり、これこそが電磁波であるということです。

同じように、４つ目の式の両辺を zz で微分した後、3つ目の式を代入することで、

d2Bydz2=ε0μ0d2Bydt2\frac{d^2B_y}{dz^2}=\varepsilon_0\mu_0\frac{d^2B_y}{dt^2}

が成立することがわかります。つまり、磁場も速さ 1ε0μ0\dfrac{1}{\sqrt{\varepsilon_0\mu_0}} の波になるということです。

SHARE
<
masstocharge
トムソンの実験と磁場偏向をアニメーションで見よう
elecore1
電磁気を根本から理解しよう① 〜電荷と電磁場とは〜
>
Images are created with the Desmos Graphing Calculator, used with permission from Desmos Studio PBC.
© 2024 UNS Physics. All Rights Reserved.