皆さんは電子がどのように原子核の周りに存在しているか知っていますか？今回は、物理学者のラザフォードとボーアが考えた電子の姿を、アニメーションで見てみましょう！

アニメーション

詳しくは後述しますが、ラザフォードは原子核の周りを電子が公転していると考えました。その後ボーアは、電子は波として振る舞っていると考えました。

ラザフォード ボーア と書かれたスイッチを入れて、それぞれが描いた電子の姿を見てみましょう！

吸収 放出 と書かれたスイッチを押すと、光子を吸収したり放出したりさせることができます。こちらも詳しくは後述します。

原子の姿は謎だった

物質が原子という粒から形成されているという考え方は古くから存在していました。しかし、原子の中で正電荷や負電荷がどのように存在しているのかは謎となっていました。

当時わかっていたこととしては、正電荷と負電荷が同じだけ存在することで原子全体が電気的に中性になっていること、原子の質量のほとんどは正電荷が持っているであろうということ、そして原子は特定の周波数の電磁波を吸収・放出することなどです。

これらの情報をもとに、様々な物理学者がいろいろな仮説を立てていきました。

様々な原子模型

トムソンのブドウパンモデル

1904年、トムソンはブドウパンモデルを発表しました。

名前の通りブドウパンを模したもので、大きく広がった正電荷の中に小さな負電荷がブドウのように散らばっているというものです。

長岡の土星型モデル

同じく1904年に長岡半太郎は土星型モデルを発表しました。

これは、まるで土星の輪のように大きな正電荷の周りを無数の電子がリング上に公転しているというものです。

ラザフォードのモデル

ラザフォードは金箔に $\alpha$ 粒子をぶつけまくるという実験を通して、ブドウパンモデルを否定しました。

$\alpha$ 粒子は電荷をもった小さな粒子ですが、ほとんどの粒子は金箔を通り抜け、ごく一部の粒子だけが金箔に大きく散乱されるという実験結果となりました。

この実験結果はブドウパンモデルをもとにすると説明できません。ブドウパンモデルでは正電荷は大きく（薄く）広がっているので、 $\alpha$ 粒子はあまり影響を受けずにそのまま通過するはずであり、一部の粒子が大きく散乱される現象をうまく説明することができません。

そこで、ラザフォードは正電荷（原子核）は小さく中心に存在していて、その周りを電子が公転しているというモデルを発表しました。

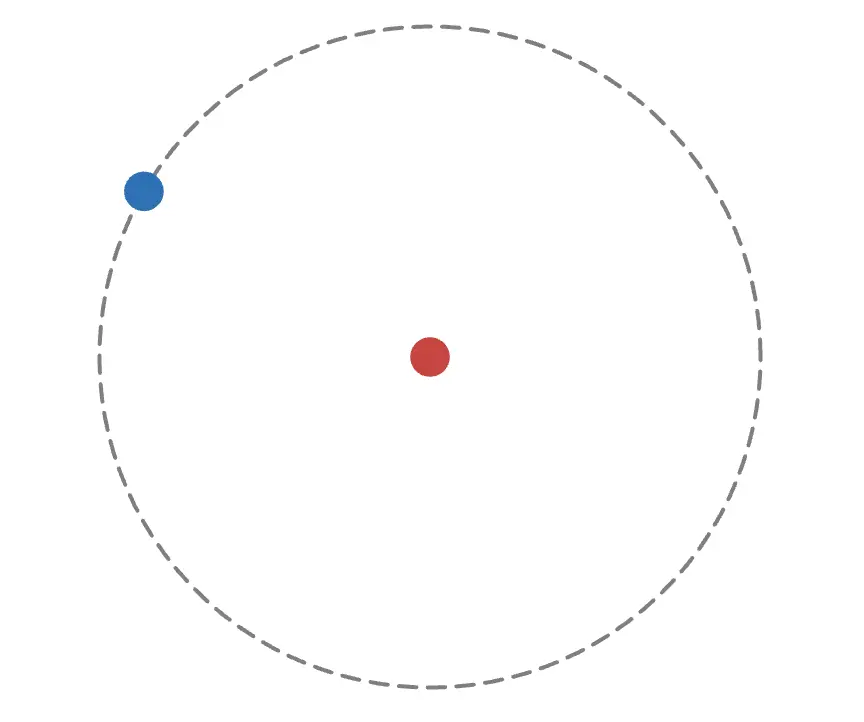
このモデルであれば、$\alpha$ 粒子は中心の小さい正電荷に衝突した時のみ、大きく散乱すると考えられるので、実験結果を上手く説明することができます。

これは高校化学でも教わる有名なモデルですが、実はいくつか難点を含んでいます。

難点①：電子が原子核に落ちてしまう

電磁気学によると、加速度を持った電荷は周りに電磁波を放出してエネルギーを失ってしまうことがわかります。

ラザフォードのモデルでは電子は円運動をしているので、中心向きの加速度を持っています。つまり、電磁波を周りに放出してエネルギーを失ってしまいます。

エネルギーを失った電子は速度を減らして原子核へと落ちていってしまうはずですが、現実だとそのようなことは起きません。

難点②：吸収・放出する電磁波が連続的

原子は特定の振動数の電磁波を吸収・放出できることがわかっていました。

しかし、ラザフォードのモデルでは電子が連続的にどのような速さを取ることもできるため、電子から放出される電磁波はどんな振動数を取ることもできます。（単位時間あたりの円運動の回数が電磁波の振動数に等しいです）

ボーアのモデル

ボーアはこれらのラザフォードモデルの難点を解決できるモデルを提唱しました。

それは、電子はとある条件を満たす半径上でしか運動できないというものです。とある条件とは、

です。これは量子条件と呼ばれます。ただし、$m$ は電子の質量、$v$ は電子の速さ、$r$ は公転半径、$h$ はプランク定数です。$n$ は任意の自然数であり、これを量子数と言います。

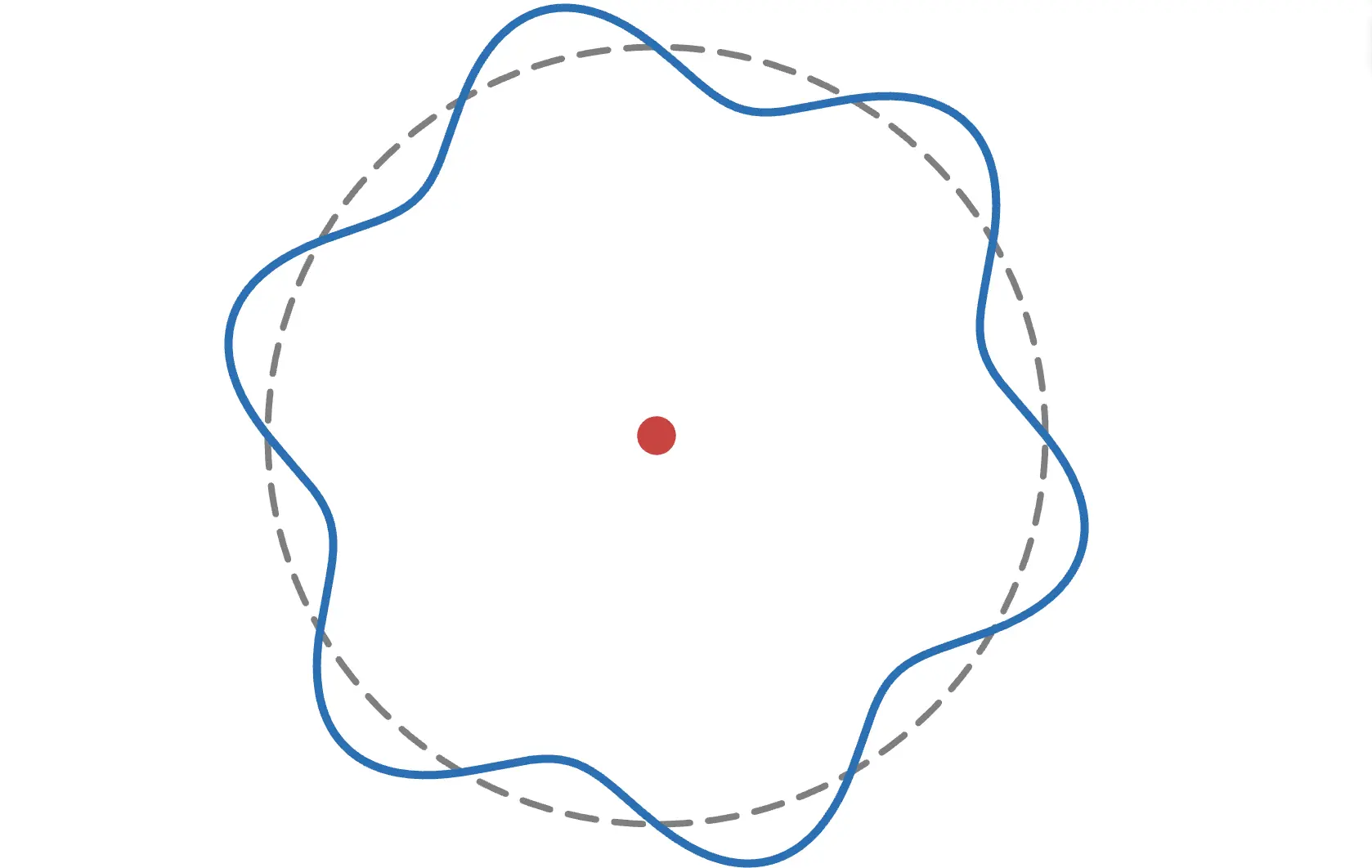
これだけだと何を意味するかがわかりにくいです。しかし、電子は物質波という波としての性質を持つことを踏まえると、電子は波（定在波）として原子核の周りに存在していると考えることができます。

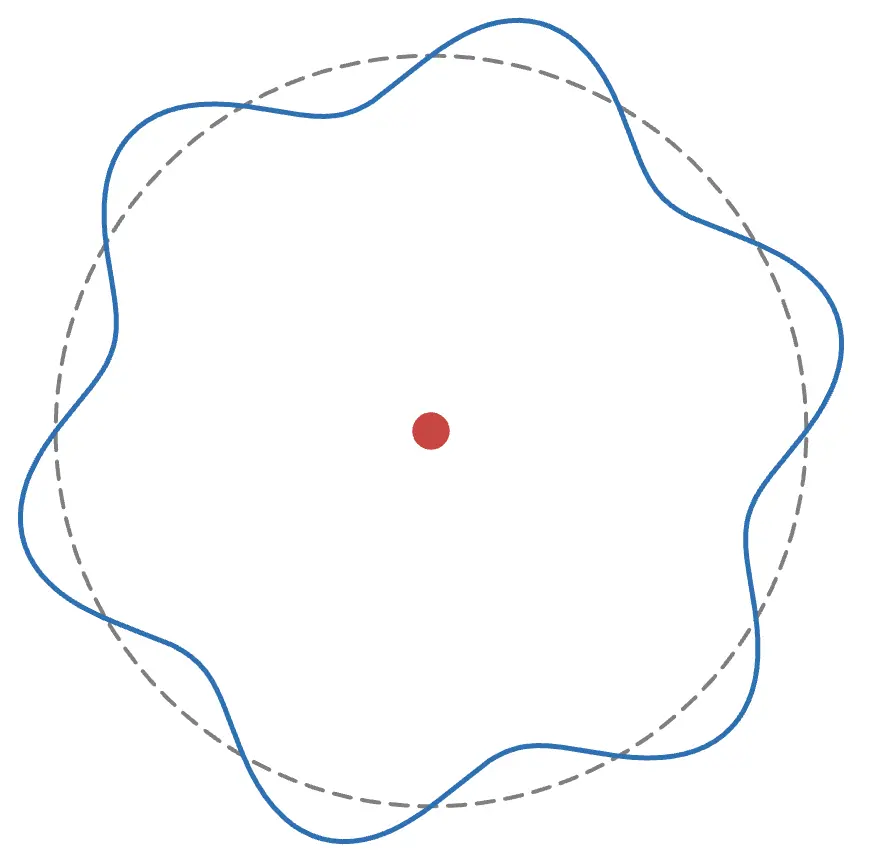
上の図のように波を形成するには、円周の長さが電子の波長の整数倍である必要があります。例えば、円周が中途半端な長さだとこのようになります。

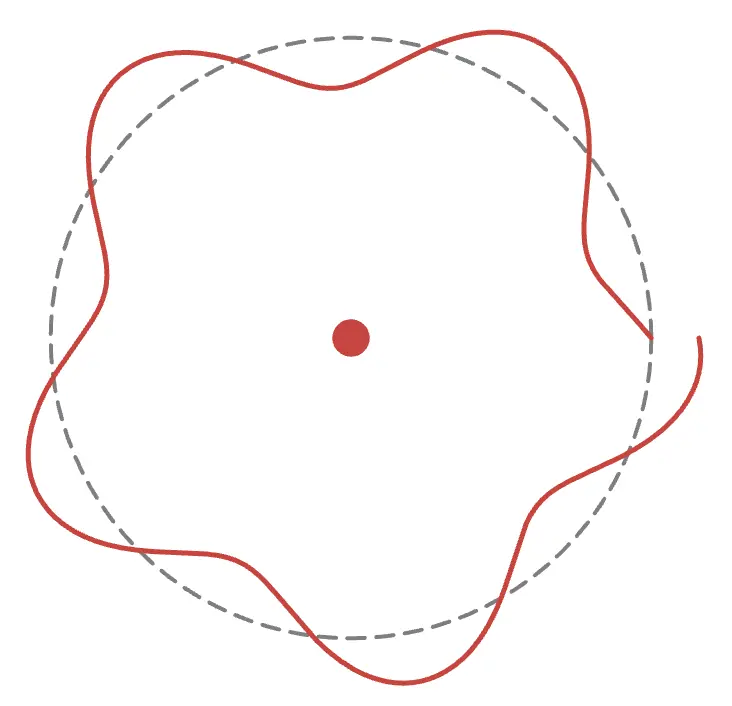
波が上手くつながらず、安定して存在できません。ぜひ、アニメーションの半径を色々といじってみてください！

つまり、円周の長さが電子の波長の整数倍であることより、

が成立します。ここに、物質波について成り立つ式 $mv=h/\lambda$ を代入することで、先ほどの量子条件を導くことができます！高校物理だとこの式を量子条件と呼ぶことも多いです。

この量子条件により、電子が原子核へと落ちていかない理由が説明できました。実はそれだけでなく、電子が吸収・放出する電磁波の振動数がとびとびの値になることも説明できます！

電子がある半径から違う半径に移ることを考えます。それぞれの半径の時に持つ運動エネルギーや位置エネルギーは当然異なります。量子数が $n$ の時の半径を $r_n$ 、電子が持つエネルギーを $E_n$ とします。

電子が $r_n$ から $r_{n'}$ に移る時、その差分のエネルギー $|E_{n'}-E_n|$ を光子として吸収・放出すると考えると全てうまくいきます！グラフしたの 吸収１ ボタンを押してみてください！

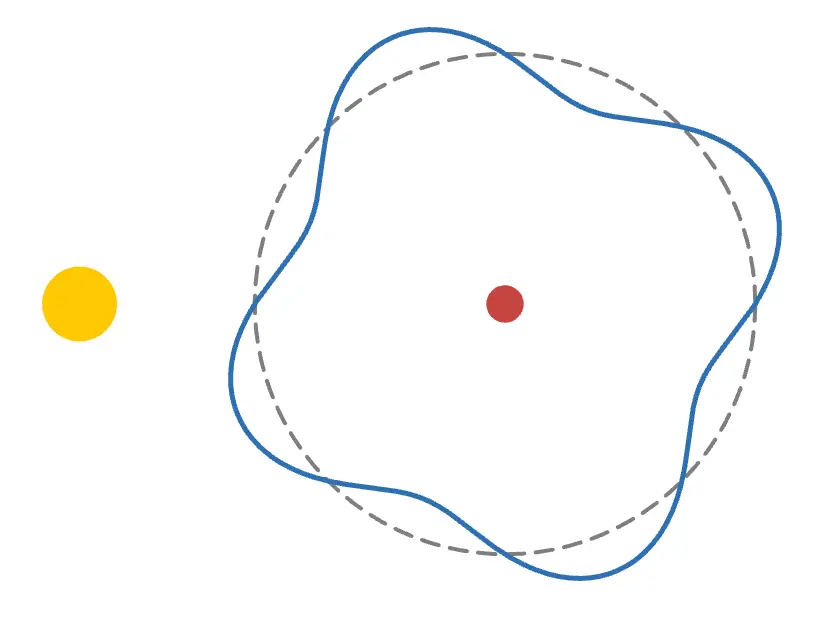
上の図のように光子が電子へと飛んでいき、

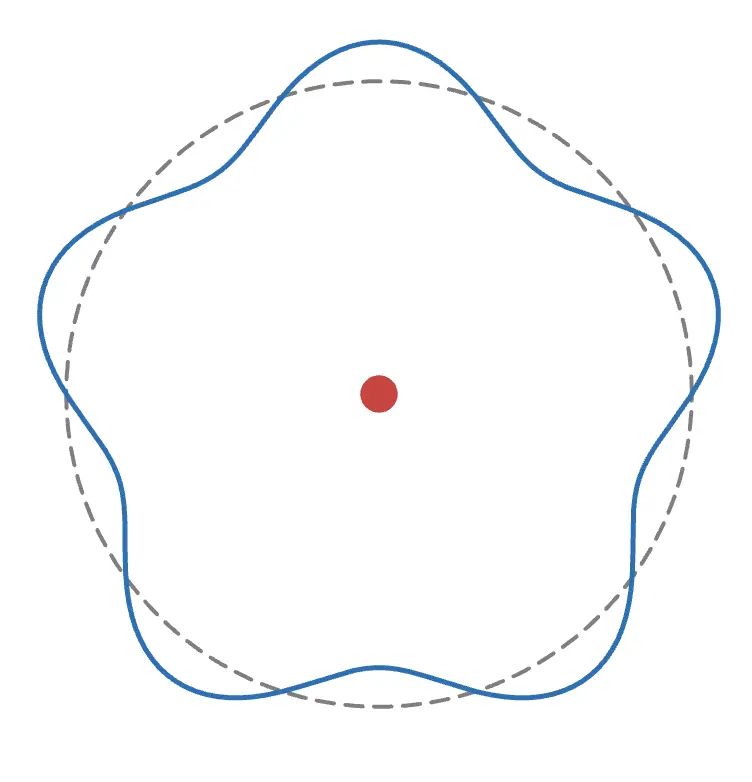
電子に光子が吸収され、電子の波が１つ増えて、半径もその分大きくなります。

波は１つずつ増えるというわけではありません。吸収２ ボタンを押すと、波が一気に2個増える様子が観察できます。

この時吸収される光子は、$E_{n'}-E_n$ のエネルギーを持っているわけですが、これが振動数 $\nu$ を用いて $h\nu$ とも表されるわけなので、

を満たす振動数の光子しか吸収されないという仕組みです。

光子が放出される場合は逆です。放出される光子のエネルギーは $E_{n}-E_{n'}$ であるので、光子の振動数は

に限られます。

実際の原子の姿

これらはニュートン力学を前提としたモデルでしたが、現実ではミクロな粒子は量子力学に従った振る舞いをすることが現在は分かっています。

数々の実験により、電子の位置や運動量といった物理量は確率でしか決まらないことが明らかになりました。よって、これまでの電子の位置が常に定まっているとした考え方は誤っていることが分かっています。

実際には、電子の存在確率がまるで雲のように原子核の周りに分布しています。詳しくは量子力学について調べてみてください！