振動数が近い２つの波が重ね合わさると うなり という現象が発生することを知っていますか？今回はうなりを見て聴いて遊んでみましょう！

うなりを聴こう

iPhone などでこのページを開いていて音が聞こえない場合は、ミュートを解除してから 再生/停止 ボタンを押してください。

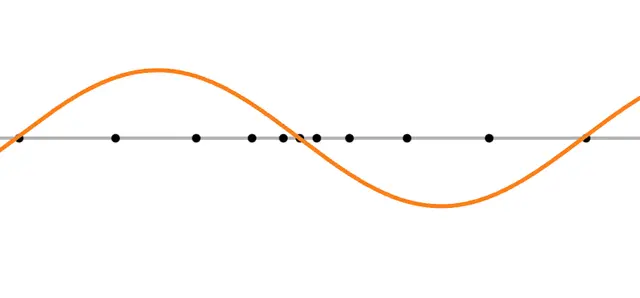
上の２つの波は、重ね合わさる２つの波を表しています。下にある紫色の波が、その合成波（実際に聞こえる波）を表しています

振動している黒い点の位置に、皆さんが立っていると考えてください。つまり、黒い点の振動が皆さんが実際に耳で感じ取っている空気の振動を表します。

うなりとは

前述したように、うなりとは振動数が近い２つの波が重ね合わさると発生する物理現象です。

その特徴はなんといっても、その形にあります。

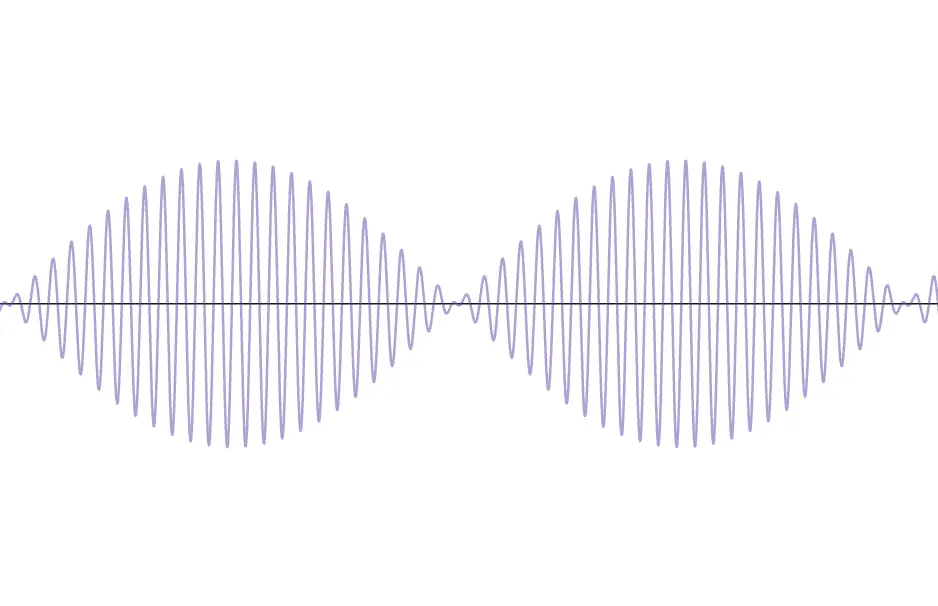
図のように、振動数の近い２つの正弦波が重ね合わさると、いくつかの塊からできたような波になります。正確に言うと、波の振幅が周期的に変化するような波になります。

音量は振幅が大きいほど大きくなります。うなりは振幅の大きさが周期的に変化しているので、音量も周期的に変化します。

その結果として、ウワンウワンといった特徴的な音が聞こえるというわけです。

式で導出

では、なぜこのような現象が起こるのかを計算で確認してみましょう！

まず、振動数が $f\ [\mathrm{Hz}]$ 、速さが $v\ [\mathrm{m/s}]$ の正弦波の変位は

と表すことができます。

ここで、振動数が $f_1,f_2\ [\mathrm{Hz}]$ の２つの波

を重ね合わせることを考えます。ただし２つの振動数は近いため、$f_1\fallingdotseq f_2$ が成立します。

合成波を $y_{\textrm{合}}(x,t)\ [\mathrm{m}]$ と書くことにすると、

なんだか複雑な式になりました...

この最後の式を観察してみると、２つの波の積になっていることが分かります。

音の高さを決める波

まず、最初の波

について考察してみます！

これは、振動数が $\dfrac{f_1+f_2}2\ [\mathrm{Hz}]$ である波になっています。つまり、重ね合わせた２つの波の振動数の平均をとった音になるわけです。

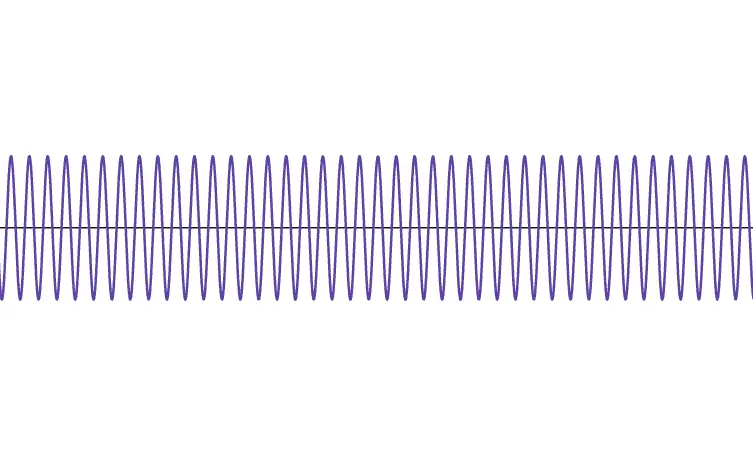
うなりを表す波

重要なのは２つ目の波

です。これは振動数が $\dfrac{|f_1-f_2|}2\ [\mathrm{Hz}]$ である波を表しています。

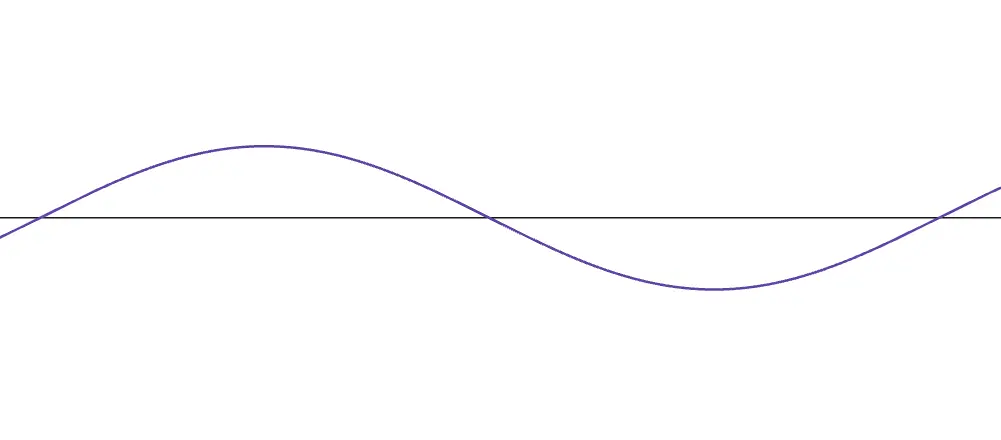
$f_1\fallingdotseq f_2$ であったことを考えると、この振動数はとても小さい値になっていることが分かります。つまり、図のように波長はとても大きくなります。

２つの波の積

では、その積である合成波はどのようなものになるでしょうか？

先ほどまでの２つの波をそのまま掛け合わせることを考えると、このような波になります。

この時、先端を結ぶと２つ目の波長の大きい波の形になっていることに注目してください！（厳密には振幅を２倍したものです）

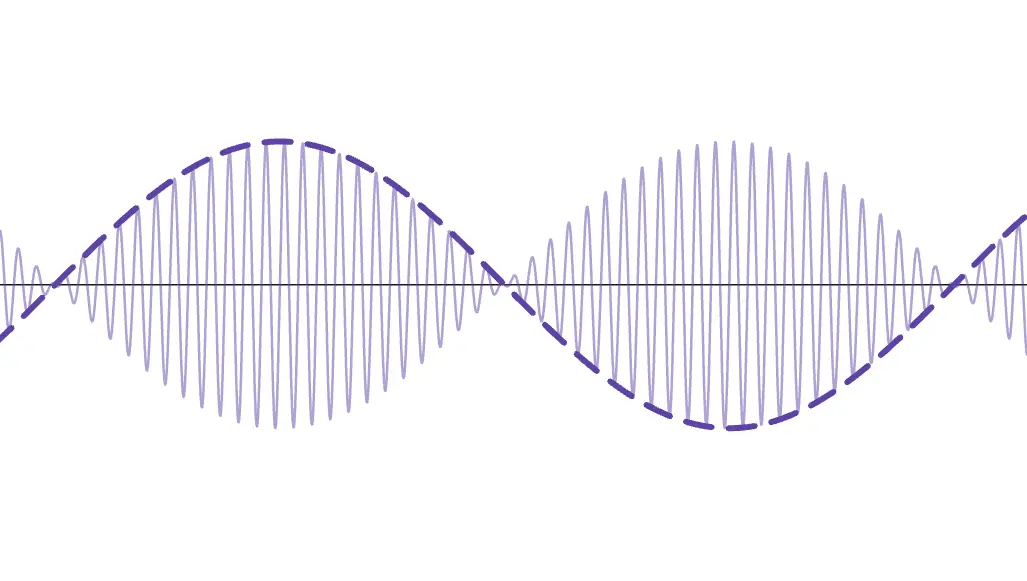
つまり、２つ目の波長の長い波によって、波の振幅が周期的に変化することで うなり となるわけです！

うなりの振動数

では、うなりの振動数を求めてみましょう。

ここで言ううなりの振動数とは、音量（＝振幅）が単位時間あたりに何回振動するかを表します。つまり、１秒間に何回ウワンとうなるかを求めます。

注目するのは２つ目の波

です。

この波の振動数は $\dfrac{|f_1-f_2|}2\ [\mathrm{Hz}]$ でしたが、これはうなりの振動数ではありません。

この波が１回振動するごとに、うなりは２回振動します！つまり、

がうなりの振動数になります！

身近なうなり

身近なうなりの現象として、ピアノにおける不協和音があげられます。

ピアノで隣り合う２つの音（シとドなど）を同時に鳴らすと、不協和音と呼ばれる不快な音が発生します。これは、隣り合う音の振動数が近いことによって発生したうなりのせいであると捉えることができます。

詳しくは、以下の記事をご覧ください！

【聴いて実感】綺麗な/汚い和音と波の関係