【運動方程式】加速度や力をグラフで理解しよう

作成日：2025/3/27

加速度や力といった概念は力学の一番の基本ですが、最初はなかなか実感しにくいと思います。今回はグラフを通して加速度や力を実感し、それらを結びつける運動方程式を理解しましょう！

グラフ

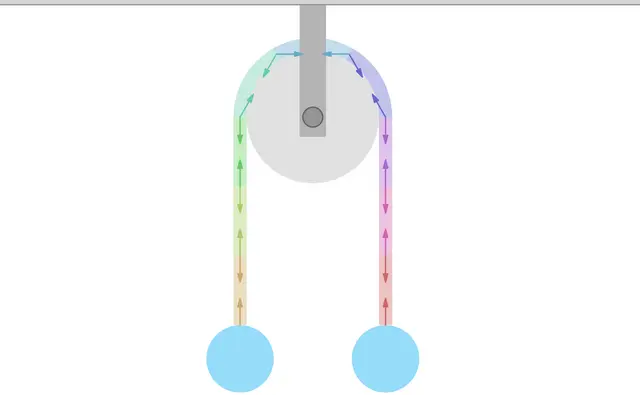
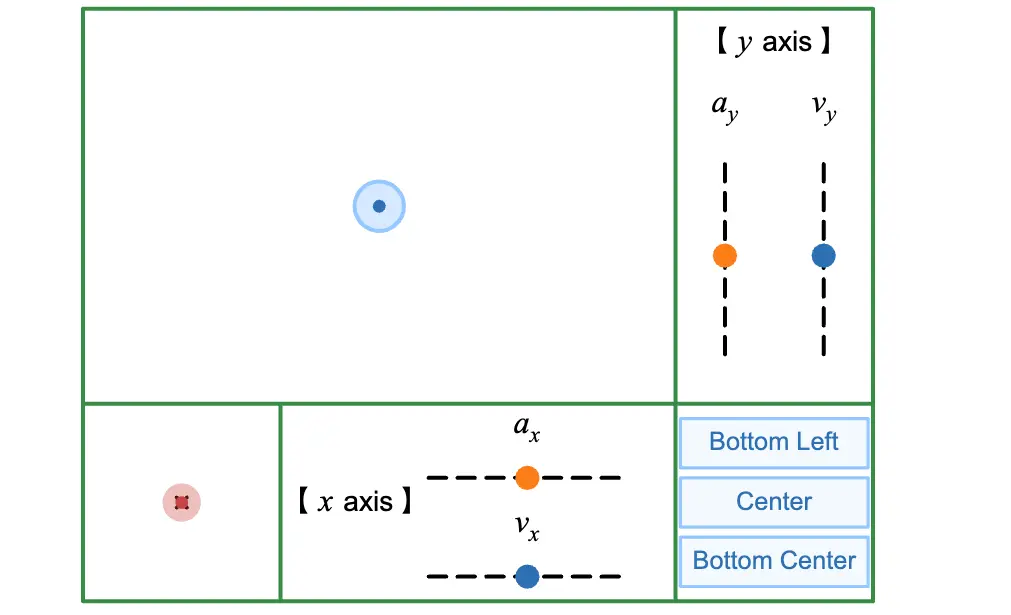
左下の赤い点をドラッグしてみてください！ドラッグした方向に力が加わるようになっています。

背景の円

質量

Desmos のグラフはこちら
グラフのみを表示

$x,\,y$ 方向の加速度と速度をそれぞれスライダーで確認できます。右下のボタンを押すと物体の位置をリセットできます。

また、物体の質量をスライダーで調整できます。質量については後述します。

背景の円 と書かれたスイッチをいれると背景に円が出現します。円の灰色の部分に触れないように物体を１周させられるかも試してみてください！（円運動については別の記事で解説する予定です。）

加速度とは

加速度について理解する前に、まずは速度について理解しましょう。

中学校までは距離÷時間が速度であると習ったと思いますが、きちんと速度を定義すると、単位時間あたりの位置の変化量であると言えます。単位時間というとわかりにくいので、１秒あたりの位置の変化量と考えても良いです。例えば１秒間に 3m 進むならば、速度は秒速 3m です。これは $3\,\mathrm{m/s}$ と書きます。 $\mathrm s$ は秒secondのことです。

では加速度とは何でしょうか？加速度は、単位時間あたりの速度の変化量と定義できます。つまり、１秒あたりに速度がどれだけ変化するかを表す量です。

例えば、最初の速度が $2\,\mathrm{m/s}$ であった物体が、 $1\,\mathrm s$ 経つうちに $5\,\mathrm{m/s}$ に変化したとします。このときは $1\,\mathrm s$ 間に速度が $3\,\mathrm{m/s}$ 変化したわけなので、加速度は $3\,\mathrm{m/s^2}$ となります。

加速度は英語で acceleration といいますが、まさに自動車のアクセルをイメージしてほしいです。アクセルを踏むと、自動車は段々と速度が上がりますよね？つまりアクセルを踏むことは自動車に加速度を与えることと同じです。

速度の単位は $\mathrm{m/s}$ でしたが、加速度は速度を時間で割ったものなので、単位は $\mathrm{m/s^2}$ となります。

この速度・加速度は、微分を用いると厳密に定義できます。物体の位置を $r$ 、速度を $v$ 、加速度を $a$ 、時刻を $t$ とすると、

v=\frac{dr}{dt},\quad a=\frac{dv}{dt}

となります。つまり、速度は位置を時間で１回微分したもの、加速度は速度を時間で１回微分したものです。

また、とても大事なポイントとして、速度も加速度も向きを持っています。これまでは一方向のみに動くことを考えていましたが、実際には物体は様々な方向に動くことができます。つまり、速度や加速度は向きを持っているベクトルであるということです。

速度を $\overrightarrow{v}$ 、加速度を $\overrightarrow{a}$ とすると、

\left(\overrightarrow{v}=\frac{d\overrightarrow r}{dt},\right)\quad \overrightarrow a=\frac{d\overrightarrow v}{dt}

が一番正確な速度と加速度の定義です。（位置 $\overrightarrow r$ もそれぞれの方向の成分を持っているので、ベクトルです）

このようにベクトル表記だとイメージが湧きにくいかもしれませんが、これは単にそれぞれの方向の成分を微分しているだけです。つまり、

\overrightarrow a=\frac{d\overrightarrow v}{dt}=\left(\frac{dv_x}{dt},\frac{dv_y}{dt},\frac{dv_z}{dt}\right)

です。 $x$ 軸方向の速度の変化量が加速度の $x$ 成分になっています。

補足

速度の大きさを速さと呼ぶことが多いです。つまり、速度はベクトル量なのに対して、速さは向きを持たないスカラー量です。

力とは

物理において、力とは物体の運動を変化させるものを指します。つまり物体に力を加えると、その物体の運動が変化するということです。

もう少し細かく言うと、物体に力が加わると、その物体は力の方向に加速度を得ることができます。加速度を $\overrightarrow a$ 、力を $\overrightarrow F$ とすると、

m\overrightarrow a=\overrightarrow F

という関係が成り立ちます。ここで $m$ は物体の質量です。質量は物体の動かしにくさを表す量で、単位は $\mathrm{kg}$ です。質量が大きいほど、物体は力を受けても加速度が小さくなります。つまり、速度がなかなか変化しないので、物体は動かしにくくなるわけです。

力 $\overrightarrow F$ の単位は、 $\mathrm{kg\cdot m/s^2}$ となりますが、これを $\mathrm{N}$ ニュートンと表します。例えば、 $6\,\mathrm{N}$ の力が質量 $2\,\mathrm{kg}$ の物体に加わると、その物体は $3\,\mathrm{m/s^2}$ の加速度を得ます。

上のアニメーションにおいて、力や質量を色々と変化させてみて、加速度がどのようになるかを観察してみましょう！特に、力の向きに加速度が生まれることと、質量を増やすと加速度が小さくなって動かしにくくなることを確認してほしいです。

この式を運動方程式と呼びます。力学の最も基本となる式です。もう少し運動方程式について考察していきましょう。

運動方程式で運動を予測できる

以下、 $x$ 軸方向の成分を考えます。

運動の予測とは

力学の一番の目標は物体の運動を予測することです。これは物体の位置 $x$ を時間 $t$ の関数で表すことを指します。

例えば、物体の位置が

x(t)=3t+1

だと分かったとしましょう。すると、この物体がどの時刻にどの位置にいるかは、この式から完璧に計算することができます。時刻 $t=2$ のときの位置は、 $x(2)=7$ と求められます。他の時刻についても同様です。

このように位置 $x(t)$ を知りたいのですが、実は運動方程式を用いると求めることができます！これが運動方程式の強みです。

計算方法

まず、一般的に計算する方法を示します。よくわからなくなってしまった人は、この次の具体例を先に読むことをおすすめします。

運動方程式は

ma(t)=F(t)

でした。（ $x$ 軸方向の成分を考えているので、ベクトルでなくてもいいです）

これより、

a(t)=\frac {F(t)}m

となります。加速度は速度の時間微分であったことを思い出してください。つまり、微分と逆の操作である積分をすると、加速度から速度を導けます。具体的には、

v(t)=\int a(t)dt

となります。位置についても同様です。位置は速度を時間で積分したものなので、

x(t)=\int v(t)dt=\int \left(\int a(t)dt\right) dt

となります。ここに先程の $a(t)$ を代入すれば、

x(t)=\int \left(\int \frac {F(t)}m dt\right) dt

となり、力 $F(t)$ から位置 $x(t)$ を求めることができます！

具体例

力が常に一定で $F(t)=6\,\mathrm N$ である時を考えましょう。運動方程式は

ma(t)=6\,\mathrm N

となります。質量を $m=2\,\mathrm{kg}$ とすると、加速度は

a(t)=\frac {6\,\mathrm N}{2\,\mathrm{kg}}=3\,\mathrm{m/s^2}

と求まります。速度はこれを積分したものなので、

v(t)=\int 3\,dt=3t+C_1\ \mathrm{m/s}

となります。積分定数 $C_1$ は初速度によって決まります。もし初速度が $v(0)=2\,\mathrm{m/s}$ だったとすると、

v(t)=3t+2\ \mathrm{m/s}

となります。位置はこれをさらに積分したものなので、

x(t)=\int (3t+2)dt=\frac 32t^2+2t+C_2\ \mathrm m

となります。積分定数 $C_2$ は初期位置によって決まります。もし初期位置が $x(0)=1\,\mathrm m$ だったとすると、

x(t)=\frac 32 t^2+2t+1\ \mathrm m

となります。例えば $t=2\,\mathrm s$ における位置は、 $x(2)=9\,\mathrm m$ のように求まります。

張力って何？滑車に掛かる力？グラフできちんと理解しよう

Images are created with the Desmos Graphing Calculator, used with permission from Desmos Studio PBC.